Advertisements
Advertisements
प्रश्न
Water leaks out from an open tank through a hole of area 2 mm2 in the bottom. Suppose water is filled up to a height of 80 cm and the area of cross section of the tanks is 0.4 m2. The pressure at the open surface and at the hole are equal to the atmospheric pressure. Neglect the small velocity of the water near the open surface in the tank. (a) Find the initial speed of water coming out of the hole. (b) Find the speed of water coming out when half of water has leaked out. (c) Find the volume of eater leaked out using a time interval dt after the height remained is h. Thus find the decrease in height dh in terms of h and dt.
(d) From the result of park (c) find the time required for half of the water to leak out.
उत्तर
Given:
Area of the hole of the water tank = 2 mm2
Height of filled water, h = 80 cm
Area of the cross-section of the tanks, A = 0.4 m2
Acceleration due to gravity, g = 9.8 ms- 2
Pressure at the open surface and at the hole is equal to atmospheric pressure.
(a) Velocity of water:
V \[= \sqrt{2gh}\]
\[= \sqrt{2 \times 10 \times 0 . 80}\]
\[ = 4 m/\sec\]
(b) Velocity of water when the tank is half-filled and h \[is \frac{80}{2}, i . e . , 40 cm:\]
\[= \sqrt{2 \times 10 \times 0 . 40}\]
\[ = \sqrt{8} m/\sec\]
(c) Volume:
Volume = Ah =A v dt
\[ = A \times \sqrt{2gh} dt\]
\[ = \left( 2 {mm}^2 \right)\sqrt{2gh}dt\]
Volume of the tank = Ah = V (say)
\[i . e . , \frac{dV}{dt} = A\frac{dh}{dt}\]
\[a_1 v_1 = A\frac{dh}{dt}\]
\[ \Rightarrow 2 \times {10}^{- 6} \sqrt{2gh} = 0 . 4\frac{dh}{dt}\]
\[ \Rightarrow dh = 5 \times {10}^{- 6} \sqrt{2gh}dt\]
\[(d) \because dh = 5 \times {10}^{- 6} \sqrt{2gh}\ dt\]
\[ \therefore \frac{dh}{\sqrt{2gh}} = 5 \times {10}^{- 6}\ dt\]
On integrating, we get:
\[5 \times {10}^{- 6} \int_0^t dt = \frac{1}{\sqrt{28}} \int_{0 . 8}^{0 . 4} \frac{dh}{\sqrt{h}}\]
\[ = 5 \times {10}^{- 6} \times t = \frac{1}{\sqrt{28}} \times 2 \left[ h^\frac{1}{2} \right]_{0 . 8}^{0 . 4} \]
\[ = 5 \times {10}^{- 6} \times t = \frac{1}{\sqrt{28}} \times 2 \left[ h^\frac{1}{2} \right]_{0 . 8}^{0 . 4} \]
\[ \Rightarrow t = \frac{1}{\sqrt{20}} \times 2 \times \left[ (0 . 4 )^{1/2} - (0 . 8 )^{1/4} \right] \times \frac{1}{5 \times {10}^{- 6}}\]
\[ \Rightarrow t = \frac{1}{4 . 47} \times 2 \times \frac{2}{3 . 16} \times \frac{1}{5 \times {10}^{- 6}} \times \frac{1}{3600} h\]
\[ = 6 . 51 h\]
Thus, the time required to leak half of the water out is 6.51 hours.
APPEARS IN
संबंधित प्रश्न
During blood transfusion the needle is inserted in a vein where the gauge pressure is 2000 Pa. At what height must the blood container be placed so that blood may just enter the vein? [Use the density of whole blood from Table 10.1].
A barometer tube reads 76 cm of mercury. If the tube is gradually inclined keeping the open end immersed in the mercury reservoir, will the length of mercury column be 76 cm, more than 76 cm or less than 76 cm?
A one meter long glass tube is open at both ends. One end of the tube is dipped into a mercury cup, the tube is kept vertical and the air is pumped out of the tube by connecting the upper end to a suction pump. Can mercury be pulled up into the pump by this process?
A satellite revolves round the earth. Air pressure inside the satellite is maintained at 76 cm of mercury. What will be the height of mercury column in a barometer tube 1 m long placed in the satellite?
Equal mass of three liquids are kept in three identical cylindrical vessels A, B and C. The densities are ρA, ρB, ρC with ρA < ρB < ρC. The force on the base will be
Shows in the following figure a siphon. The liquid shown is water. The pressure difference PB − PAbetween the points A and B is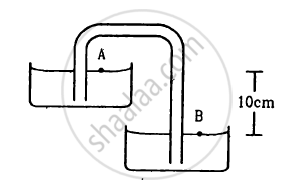
A barometer kept in an elevator reads 76 cm when it is at rest. If the elevator goes up with increasing speed, the reading will be ______.
A barometer kept in an elevator accelerating upward reads 76 cm. The air pressure in the elevator is
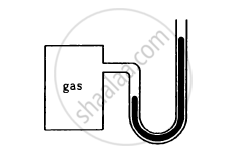
The heights of mercury surfaces in the two arms of the manometer shown in figure are 2 cm and 8 cm.
Atmospheric pressure = 1.01 × 105 N−2. Find (a) the pressure of the gas in the cylinder and (b) the pressure of mercury at the bottom of the U tube.
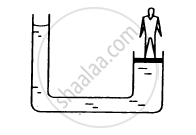
The area of cross section of the wider tube shown in figure is 900 cm2. If the boy standing on the piston weighs 45 kg, find the difference in the levels of water in the two tubes.
The weight of an empty balloon on a spring balance is W1. The weight becomes W2when the balloon is filled with air. Let the weight of the air itself be w. Neglect the thickness of the balloon when it is filled with air. Also neglect the difference in the densities of air inside and outside the balloon.
(a) W2 = W1
(b) W2 = W1 + w
(c) W2 < W1 + w
(d) W2 > W1
A glass full of water has a bottom of area 20 cm2, top of area 20 cm2, height 20 cm and volume half a litre.
(a) Find the force exerted by the water on the bottom.
(b) Considering the equilibrium of the water, find the resultant force exerted by the sides of the glass on the water. Atmospheric pressure = 1.0 × 105 N/m2. Density of water 1000 kg/m3 and g = 10 m/s2. Take all numbers
to be exact.
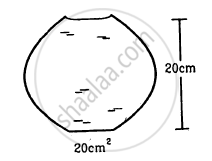
Suppose the glass of the previous problem is covered by a jar and the air inside the jar is completely pumped out. (a) What will be the answers to the problem? (b) Show that the answers do not change if a glass of different shape is used provided the height, the bottom area and the volume are unchanged.
If water be used to construct a barometer, what would be the height of water column at standard atmospheric pressure (76 cm of mercury) ?
Water is filled in a rectangular tank of size 3 m × 2 m × 1 m. (a) Find the total force exerted by the water on the bottom surface on the tank. (b) Consider a vertical side of area 2 m × 1 m. Take a horizontal strip of width δx metre in this side, situated at a depth of x metre from the surface of water. Find the force by the water on this strip. (c) Find the torque of the force calculate in part (b) about the bottom edge of this side.
(d) Find the total force by the water on this side.
(e) Find the total torque by the water on the side about the bottom edge. Neglect the atmospheric pressure and take g = 10 ms−2.
A U-tube containing a liquid is accelerated horizontally with a constant acceleration a0. If the separation between the vertical limbs is l, find the difference in the heights of the liquid in the two arms.
Pressure decreases as one ascends the atmosphere. If the density of air is ρ, what is the change in pressure dp over a differential height dh?
A glass capillary sealed at the upper end is of length 0.11 m and internal diameter 2 × 10-5 m. This tube is immersed vertically into a liquid of surface tension 5.06 × 10-2 N/m. When the length x × 10-2 m of the tube is immersed in liquid then the liquid level inside and outside the capillary tube becomes the same, then the value of x is ______ m. (Assume atmospheric pressure is 1.01 × 105 `"N"/"m"^2`)
