Advertisements
Advertisements
प्रश्न
A capillary of diameter d mm is dipped in water such that the water rises to a height of 30 mm. If the radius of the capillary is made `(2/3)` of its previous value, then compute the height up to which water will rise in the new capillary?
उत्तर
Let diameter of capillary tube = d mm
Let the radius of capillary tube r1 = r mm
Capillary rise h1 = 30 mm
Let the radius of another capillary tube r2 = `2/3` r
Let the capillary rise of another capillary tube be h2
We know that
T = `("hr"ρ"g")/2`
∴ `"h" ∝ 1/"r"`
`"h"_1/"h"_2 = "r"_2/"r"_1`
`30/"h"_2 = (2/3 "r")/"r"`
`30/"h"_2 = 2/3`
∴ h2 = `(3 xx 30)/2` = 45 mm
Capillary rise in the new capillary tube = 45 mm
APPEARS IN
संबंधित प्रश्न
Derive Laplace’s law for spherical membrane of bubble due to surface tension.
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
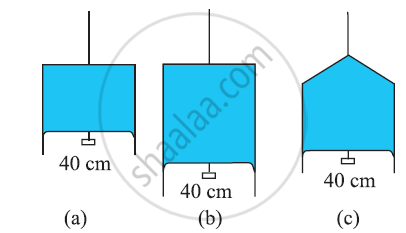
Figure (a) shows a thin liquid film supporting a small weight = 4.5 × 10–2 N. What is the weight supported by a film of the same liquid at the same temperature in Fig. (b) and (c)? Explain your answer physically.
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution in S, the work done in the process is
A metal piece of mass 160 g lies in equilibrium inside a glass of water. The piece touches the bottom of the glass at a small number of points. If the density of the metal is 8000 kg/m3, find the normal force exerted by the bottom of the glass on the metal piece.

Solve the previous problem if the lead piece is fastened on the top surface of the block and the block is to float with its upper surface just dipping into water.
A hot air balloon is a sphere of radius 8 m. The air inside is at a temperature of 60°C. How large a mass can the balloon lift when the outside temperature is 20°C? (Assume air is an ideal gas, R = 8.314 J mole–1K–1, 1 atm. = 1.013 × 105 Pa; the membrane tension is 5 Nm–1.)
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
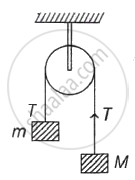
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.