Advertisements
Advertisements
प्रश्न
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
उत्तर
Given:
Density of wood, ρw = 0.8 gm/cc
Density of lead, ρpb = 11.3 gm/cc
Weight of the cubical wood block, mw = 200 g
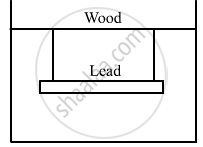
The cubical block floats in water.
Now,
(mw+ mpb) × g = (Vw + Vpb)ρ × g
Here,
ρ = Density of water
Vw = Volume of wood
Vpb = Volume of lead
\[\Rightarrow ( \text{m}_\text{w} + \text{m}_{\text{pb}} ) = \left( \frac{\text{m}_\text{w}}{\rho_\text{w}} + \frac{\text{ m}_{\text{pb}}}{\rho_{\text{pb}}} \right)\rho\]
\[ \Rightarrow (200 + \text{m}_{\text{pb}} ) = \left( \frac{200}{0 . 8} + \frac{\text{m}_{\text{pb}}}{11 . 3} \right) \times 1\]
\[ \Rightarrow \text{m}_{\text{pb}} - \frac{\text{m}_{\text{pb}}}{11 . 3} = 250 - 200\]
\[ \Rightarrow \frac{10 . 3 \text{m}_{\text{pb}}}{11 . 3} = 50\]
\[ \Rightarrow \text{m}_{\text{pb}} = \frac{50 \times 11 . 3}{10 . 3} = 54 . 8 \text{ gm }\]
APPEARS IN
संबंधित प्रश्न
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
Explain why The angle of contact of mercury with glass is obtuse, while that of water with glass is acute
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than 90°. Explain.
When the size of a soap bubble is increased by pushing more air in it, the surface area increases. Does it mean that the average separation between the surface molecules is increased?
Water rises in a vertical capillary tube up to a length of 10 cm. If the tube is inclined at 45°, the length of water risen in the tube will be
A liquid is contained in a vertical tube of semicircular cross section. The contact angle is zero. The force of surface tension on the curved part and on the flat part are in ratio
A cubical block of ice floating in water has to support a metal piece weighing 0.5 kg. Water can be the minimum edge of the block so that it does not sink in water? Specific gravity of ice = 0.9.
A cubical metal block of edge 12 cm floats in mercury with one fifth of the height inside the mercury. Water in it. Find the height of the water column to be poured.
Specific gravity of mercury = 13.6.
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
The wettability of a surface by a liquid depends primarily on
Two small drops of mercury each of radius 'R' coalesce to form a large single drop. The ratio of the total surface energies before and after the change is ____________.
What is surface tension? Explain the applications of surface tension.
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
