Advertisements
Advertisements
प्रश्न
Find the surface energy of water kept in a cylindrical vessel of radius 6.0 cm. Surface tension of water = 0.075 J m−2.
उत्तर
Given:
Radius of cylindrical vessel, r = 6.0 cm = 0.06 m
Surface tension of water, T = 0.075 J/m2
Area, A = πr2 = π × (0.06)2
Surface energy = T × A
= (0.075) × (3.14) × (0.06)2
= 8.5 × 10−4 J
Therefore, the surface energy of water kept in a cylindrical vessel is 8.5 × 10−4 J.
APPEARS IN
संबंधित प्रश्न
Derive an expression for excess pressure inside a drop of liquid.
Fill in the blanks using the word(s) from the list appended with each statement
Surface tension of liquids generally . . . with temperatures (increases / decreases)
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
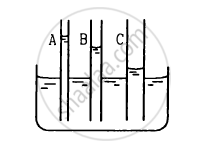
The capillaries shown in figure have inner radii 0.5 mm, 1.0 mm and 1.5 mm respectively. The liquid in the beaker is water. Find the heights of water level in the capillaries. The surface tension of water is 7.5 × 10−2 N m−1.
The lower end of a capillary tube is immersed in mercury. The level of mercury in the tube is found to be 2 cm below the outer level. If the same tube is immersed in water, up to what height will the water rise in the capillary?
A capillary tube of radius 1 mm is kept vertical with the lower end in water. (a) Find the height of water raised in the capillary. (b) If the length of the capillary tube is half the answer of part , find the angle θ made by the water surface in the capillary with the wall.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
A solid sphere of radius 5 cm floats in water. If a maximum load of 0.1 kg can be put on it without wetting the load, find the specific gravity of the material of the sphere.
How much amount of work is done in forming a soap bubble of radius r?
Numerical Problem.
A stone weighs 500 N. Calculate the pressure exerted by it if it makes contact with a surface of area 25 cm2.
How is surface tension related to surface energy?
Define the angle of contact for a given pair of solid and liquid.
A drop of oil placed on the surface of water spreads out. But a drop of water place on oil contracts to a spherical shape. Why?
The angle of contact at the interface of water-glass is 0°, Ethylalcohol-glass is 0°, Mercury-glass is 140° and Methyliodide-glass is 30°. A glass capillary is put in a trough containing one of these four liquids. It is observed that the meniscus is convex. The liquid in the trough is ______.
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
A drop of water and a soap bubble have the same radii. Surface tension of soap solution is half of that of water. The ratio of excess pressure inside the drop and bubble is ______.
Work done to blow a bubble of volume V is W. The work done in blowing a bubble of volume 2V will be ______.
Define angle of contact.
