Advertisements
Advertisements
Question
A raindrop of diameter 4 mm is about to fall on the ground. Calculate the pressure inside the raindrop. [Surface tension of water T = 0.072 N/m, atmospheric pressure = 1.013 x 105 N/m2 ]
Solution
Given:
T = 0.072 N/m,
d = 4mm ∴ r = 2 * 10-3 m,
Po = 1.013 * 105 N/m2
To find: Pressure inside the raindrop (Pi)
Formula: Pi = Po + 2T/r
Calculation: From formula,
`P_i=1.013xx10^5+(2xx0.072)/(2xx10^(-3))`
`P_i=1.013xx10^5+0.072xx10^3`
`=1.013xx10^5+0.00072xx10^5`
`thereforeP_i=1.01372xx10^5Pa`
The pressure inside the raindrop is 1.01372 * 105 Pa.
APPEARS IN
RELATED QUESTIONS
Angle of contact for the pair of pure water with clean glass is _______.
Water rises to a height 3.2 cm in a glass capillary tube. Find the height to which the same water will rise in another glass capillary having half area of cross section.
In which of the following substances, surface tension increases with increase in temperature ?
- Copper
- Molten copper
- Iron
- Molten iron
'n' droplets of equal size of radius r coalesce to form a bigger drop of radius R. The energy liberated is equal to...................
(T =Surface tension of water)
`(a) 4piR^2T[n^(1/3)-1]`
`(b) 4pir^2T[n^(1/3)-1]`
`(c) 4piR^2T[n^(2/3)-1]`
`(d)4 pir^2T[n^(2/3)-1]`
Explain why Water on a clean glass surface tends to spread out while mercury on the same surface tends to form drops. (Put differently, water wets glass while mercury does not.)
Explain why A drop of liquid under no external forces is always spherical in shape
A U-shaped wire is dipped in a soap solution and removed. The thin soap film formed between the wire and the light slider supports a weight of 1.5 × 10–2 N (which includes the small weight of the slider). The length of the slider is 30 cm. What is the surface tension of the film?
Show that the surface tension of a liquid is numerically equal to the surface energy per unit
area.
When a sparingly soluble substance like alcohol is dissolved in water, surface tension of water
The free surface of a liquid resting in an inertial frame is horizontal. Does the normal to the free surface pass through the centre of the earth? Think separately if the liquid is (a) at the equator (b) at a pole (c) somewhere else.
It is said that a liquid rises or is depressed in capillary due to the surface tension. If a liquid neither rises nor depresses in a capillary, can we conclude that the surface tension of the liquid is zero?
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
Water near the bed of a deep river is quiet while that near the surface flows. Give reasons.
A heavy mass is attached to a thin wire and is whirled in a vertical circle. The wire is most likely to break
By a surface of a liquid we mean
An ice cube is suspended in vacuum in a gravity free hall. As the ice melts it
When water droplets merge to form a bigger drop
Air is pushed into a soap bubble of radius r to double its radius. If the surface tension of the soap solution in S, the work done in the process is
If more air is pushed in a soap bubble, the pressure in it
A 20 cm long capillary tube is dipped in water. The water rises up to 8 cm. If the entire arrangement is put in a freely falling elevator, the length of water column in the capillary tube will be
The rise of a liquid in a capillary tube depends on
(a) the material
(b) the length
(c) the outer radius
(d) the inner radius of the tube
Find the excess pressure inside (a) a drop of mercury of radius 2 mm (b) a soap bubble of radius 4 mm and (c) an air bubble of radius 4 mm formed inside a tank of water. Surface tension of mercury, soap solution and water are 0.465 N m−1, 0.03 N m−1 and 0.076 N m−1 respectively.
Consider a small surface area of 1 mm2 at the top of a mercury drop of radius 4.0 mm. Find the force exerted on this area (a) by the air above it (b) by the mercury below it and (c) by the mercury surface in contact with it. Atmospheric pressure = 1.0 × 105 Pa and surface tension of mercury = 0.465 N m−1. Neglect the effect of gravity. Assume all numbers to be exact.
A cubical box is to be constructed with iron sheets 1 mm in thickness. What can be the minimum value of the external edge so that the cube does not sink in water? Density of iron = 8000 kg/m3 and density of water = 1000 kg/m3.
A cubical block of wood weighing 200 g has a lead piece fastened underneath. Find the mass of the lead piece which will just allow the block to float in water. Specific gravity of wood is 0.8 and that of lead is 11.3.
The energy stored in a soap bubble of diameter 6 cm and T = 0.04 N/m is nearly ______.
How much amount of work is done in forming a soap bubble of radius r?
Explain the capillary action.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Insect moves over the surface of water because of ______.
The water droplets are spherical in free fall due to ______
Water rises to a height of 20 mm in a capillary tube. If the radius made 1/3rd of its previous value, to what height will the water now rise in the tube?
Two soap bubbles have a radius in the ratio of 2:3. Compare the works done in blowing these bubbles.
How does the friction arise between the surfaces of two bodies in relative motion?
A certain number of spherical drops of a liquid of radius R coalesce to form a single drop of radius R and volume V. If T is the surface tension of the liquid, then
Explain elasticity using intermolecular forces.
Distinguish between cohesive and adhesive forces.
What are the factors affecting the surface tension of a liquid?
What is capillarity?
Obtain an expression for the surface tension of a liquid by the capillary rise method.
Water rises in a capillary tube of radius r upto a height h. The mass of water in a capillary is m. The mass of water that will rise in a capillary of radius `"r"/4` will be ______.
Two spherical rain drops reach the surface of the earth with terminal velocities having ratio 16 : 9. The ratio of their surface area is ______.
Water rises upto a height h in a capillary tube on the surface of the earth. The value of h will increase, if the experimental setup is kept in [g = acceleration due to gravity]
If the surface tension of a soap solution is 3 × 10-2 N/m then the work done in forming a soap film of 20 cm × 5 cm will be ______.
Under isothermal conditions, two soap bubbles of radii 'r1' and 'r2' coalesce to form a big drop. The radius of the big drop is ______.
Is surface tension a vector?
The sap in trees, which consists mainly of water in summer, rises in a system of capillaries of radius r = 2.5 × 10–5 m. The surface tension of sap is T = 7.28 × 10–2 Nm–1 and the angle of contact is 0°. Does surface tension alone account for the supply of water to the top of all trees?
If a drop of liquid breaks into smaller droplets, it results in lowering of temperature of the droplets. Let a drop of radius R, break into N small droplets each of radius r. Estimate the drop in temperature.
Surface tension is exhibited by liquids due to force of attraction between molecules of the liquid. The surface tension decreases with increase in temperature and vanishes at boiling point. Given that the latent heat of vaporisation for water Lv = 540 k cal kg–1, the mechanical equivalent of heat J = 4.2 J cal–1, density of water ρw = 103 kg l–1, Avagadro’s No NA = 6.0 × 1026 k mole–1 and the molecular weight of water MA = 18 kg for 1 k mole.
- Estimate the energy required for one molecule of water to evaporate.
- Show that the inter–molecular distance for water is `d = [M_A/N_A xx 1/ρ_w]^(1/3)` and find its value.
- 1 g of water in the vapor state at 1 atm occupies 1601 cm3. Estimate the intermolecular distance at boiling point, in the vapour state.
- During vaporisation a molecule overcomes a force F, assumed constant, to go from an inter-molecular distance d to d ′. Estimate the value of F.
- Calculate F/d, which is a measure of the surface tension.
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
When an air bubble of radius r rises from the bottom to the surface of a lake, its radius becomes `(5r)/4`. Taking the atmospheric pressure to be equal to the 10 m height of the water column, the depth of the lake would approximately be ______.
(ignore the surface tension and the effect of temperature)
The excess pressure inside a liquid drop is 500 Nm-2. If the radius of the drop is 2 mm, the surface tension of the liquid is x × 10-3 Nm-1. The value of x is ______.
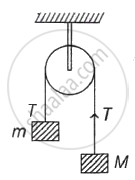
Two blocks of masses m and M are connected by means of a metal wire of cross-sectional area A passing over a frictionless fixed pully as shown in the figure. The system is then released. If M = 2m, then the stress produced in the wire is ______.
Find the work done when a drop of mercury of radius 2 mm breaks into 8 equal droplets. [Surface tension of mercury = 0.4855 J/m2].
Calculate (i) the pressure due to the weight of the water at a depth of 2.5 m and (ii) the depth below the surface of water at which the pressure due to the weight of the water equals 1.0 atm.
The surface tension of boiling water is ______.
