Advertisements
Advertisements
Question
Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.
Solution
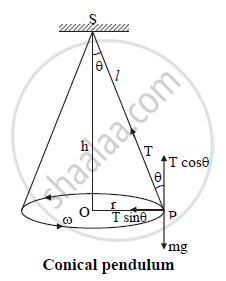
Where, S: rigid support
T : tension in the string
l : length of string
h : height of support from bob
v : velocity of bob
r : radius of horizontal circle
θ: semi-vertical angle
mg : weight of bob
i) Consider a bob of mass m tied to one
end of a string of length ‘l’ and other
the end is fixed to a rigid support.
ii) Let the bob be displaced from its mean
position and whirled around a
horizontal circle of radius ‘r’ with
constant angular velocity ω, then the
bob performs U.C.M.
iii) During the motion, a string is inclined to
the vertical at an angle θ as shown in
the above figure.
iv) In the displaced position P, there are two
forces acting on the bob.
a. The weight mg acting vertically
downwards.
b. The tension T acting upward
along the string.
v) The tension (T) acting in the string can
be resolved into two components:
a. T cos θ acting vertically upwards.
b. T sin θ acting horizontally towards
centre of the circle.
vi) Vertical component T cos θ balances the
weight and horizontal component T sin θ
provides the necessary centripetal force.
∴ T cos θ = mg . ........(1)
T sin θ = `"mv"^2/"r" = "mr"omega^2` ....(2)
vii) Dividing equation (2) by (1),
tan θ = `"v"^2/"rg"` ......(3)
Therefore, the angle made by the string with the vertical is θ = `tan^-1 ("v"^2/"rg")`
Also, from equation (3),
v2 = rg tan θ
∴ v = `sqrt ("rg" tan theta)`
The period, T = `(2pi"r")/"v" = (2pi"r")/sqrt("rg" "tan" theta) = 2pi sqrt ("r"/("g tan" theta))`
It can be seen that r - = l sin θ
T = `2pi sqrt (("l sin" theta)/("g tan" theta)) = 2pi sqrt (("l cos" theta)/"g")`
The period of a conical pendulum is `2pi sqrt (("l cos" theta)/"g")`
APPEARS IN
RELATED QUESTIONS
A particle rotates in U.C.M. with tangential velocity V along a horizontal circle of diameter ‘D' . Total angular displacement of the particle in time 't' is..........
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Read the statement below carefully and state, with reason, if it is true or false:
The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
A cyclist is riding with a speed of 27 km/h. As he approaches a circular turn on the road of radius 80 m, he applies brakes and reduces his speed at the constant rate of 0.50 m/s every second. What is the magnitude and direction of the net acceleration of the cyclist on the circular turn?
Explain the meaning of uniform circular motion. Give one example of such motion.
Give an example of motion in which speed remains uniform, but the velocity changes.
Differentiate between uniform linear motion and uniform circular motion.
| A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the centre of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre. |
- What will be your observation when you are standing outside the disc? Explain.
- What will be your observation when you are standing at the centre of the disc? Explain.
The motion of the moon around the earth in a circular path is an accelerated motion.
A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
Answer the following question.
Show that its time period is given by, 2π`sqrt((l cos theta)/("g"))` where l is the length of the string, θ is the angle that the string makes with the vertical, and g is the acceleration due to gravity.
Solve the following problem.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
Is the uniform circular motion accelerated? Give reasons for your answer.
The angle subtended by the vector A = `5hat"i" + 3hat"j" + 12hat"k"` with the X-axis is ______.
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 8 cm. The centripetal force acting on the particle is 15 N. Its kinetic energy is ____________.
A particle is moving in uniform circular motion with speed 'V' and radius 'R'. The angular acceleration of the particle is ______.
Certain neutron stars are believed to be rotating at about 1 rev/s. If such a star has a radius of 1.6 km, the acceleration of an object on the equator of the star will be nearly ____________.
Consider a simple pendulum of length 4 m. Its bob performs a circular motion in horizontal plane with its string making an angle 60° with the vertical. The Period of rotation of the bob is ____________.(Take g = 10 m/s2)
A string of length 'l' fixed at one end carries a mass 'm' at the other end. The string makes `3/pi` revolutions/second around the vertical axis through the fixed end as shown in figure. The tension 'T' in the string is ______.
A mass 'm' is tied to one end of a spring and whirled in a horizontal circle with constant angular velocity. The elongation in the spring is 1 cm. If the angular speed is doubled, the elongation in the spring is 6 cm. The original length of the spring is ______.
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
A point object moves along an arc of a circle of radius 'R'. Its velocity depends upon the distance covered 'S' as V = `Ksqrt(S)` where 'K' is a constant. If 'e' is the angle between the total acceleration and tangential acceleration, then
A particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is ______.
A wheel is rotating at 900 rpm about its axis. When the power is cut off it comes to rest in 1 min. The angular retardation (assumed to be uniform (in rad s-1) is ______.
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions, but of mass `1/4`M is placed gently on the first disc co-axially. The. angular velocity of the system is ______.
The kinetic energy K of a particle moving along a circle of radius R depends on the distance covered s as K = as2, where a is a constant. The force acting on the particle is ______.
Explain the meaning of uniform circular motion.
