Advertisements
Advertisements
प्रश्न
Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.
उत्तर
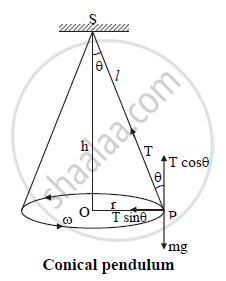
Where, S: rigid support
T : tension in the string
l : length of string
h : height of support from bob
v : velocity of bob
r : radius of horizontal circle
θ: semi-vertical angle
mg : weight of bob
i) Consider a bob of mass m tied to one
end of a string of length ‘l’ and other
the end is fixed to a rigid support.
ii) Let the bob be displaced from its mean
position and whirled around a
horizontal circle of radius ‘r’ with
constant angular velocity ω, then the
bob performs U.C.M.
iii) During the motion, a string is inclined to
the vertical at an angle θ as shown in
the above figure.
iv) In the displaced position P, there are two
forces acting on the bob.
a. The weight mg acting vertically
downwards.
b. The tension T acting upward
along the string.
v) The tension (T) acting in the string can
be resolved into two components:
a. T cos θ acting vertically upwards.
b. T sin θ acting horizontally towards
centre of the circle.
vi) Vertical component T cos θ balances the
weight and horizontal component T sin θ
provides the necessary centripetal force.
∴ T cos θ = mg . ........(1)
T sin θ = `"mv"^2/"r" = "mr"omega^2` ....(2)
vii) Dividing equation (2) by (1),
tan θ = `"v"^2/"rg"` ......(3)
Therefore, the angle made by the string with the vertical is θ = `tan^-1 ("v"^2/"rg")`
Also, from equation (3),
v2 = rg tan θ
∴ v = `sqrt ("rg" tan theta)`
The period, T = `(2pi"r")/"v" = (2pi"r")/sqrt("rg" "tan" theta) = 2pi sqrt ("r"/("g tan" theta))`
It can be seen that r - = l sin θ
T = `2pi sqrt (("l sin" theta)/("g tan" theta)) = 2pi sqrt (("l cos" theta)/"g")`
The period of a conical pendulum is `2pi sqrt (("l cos" theta)/"g")`
APPEARS IN
संबंधित प्रश्न
An aircraft executes a horizontal loop of radius 1.00 km with a steady speed of 900 km/h. Compare its centripetal acceleration with the acceleration due to gravity.
Is it possible to have an accelerated motion with a constant speed? Explain
Is it possible to have an accelerated motion with a constant speed? Name such type of motion.
A uniform circular motion is an accelerated motion. Explain it. State whether the acceleration is uniform or variable? Name the force responsible to cause this acceleration. What is the direction of force at any instant? Draw a diagram in support of your answer.
| A small pebble tied at one end of a string is placed near the periphery of a circular disc, at the centre of which the other end of the string is tied to a peg. The disc is rotating about an axis passing through its centre. |
- What will be your observation when you are standing outside the disc? Explain.
- What will be your observation when you are standing at the centre of the disc? Explain.
A uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
To which side the rule will tilt if the mass m is moved to the mark 10cm ?
Answer the following question.
Show that the centripetal force on a particle undergoing uniform circular motion is -mrω2.
If a particle moves with uniform speed then its tangential acceleration will be ______.
The ratio of angular speed of a hour-hand to the second-hand of a watch is ____________.
A particle performs uniform circular motion in a horizontal plane. The radius of the circle is 8 cm. The centripetal force acting on the particle is 15 N. Its kinetic energy is ____________.
A particle of mass m is executing uniform circular motion on a path of radius r. If p is the magnitude of its linear momentum, the radial force acting on the particle is ______.
Certain neutron stars are believed to be rotating at about 1 rev/s. If such a star has a radius of 1.6 km, the acceleration of an object on the equator of the star will be nearly ____________.
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time t?
A wheel is 0.25 m in radius. When it makes 15 revolutions per minute, its linear speed at the point on circumference is ____________.
A particle is perfonning uniform circular motion. If 'θ', 'ω', 'α' and ' a' are its angular displacement, angular velocity, angular acceleration, and centripetal acceleration respectively, then which of the following is 'WRONG'?
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
The angular speed of the minute hand of a clock in degrees per second is ______.
Which of the following is correct about uniform circular motion
- the direction of motion is continuously changed
- the direction of motion is not changed
- speed and direction both remain constant
- speed is constant but the direction is changing
A body is said to be in nonuniform motion if it travels ______.
The motion of the bus is ______ motion.
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
A ceiling fan rotates about its own axis with some angular velocity. When the fan is switched off the angular velocity becomes `(1/4)^"th"` of the original in time 't' and 'n' revolutions are made in that time. The number of revolutions made by the fan during the time interval between switch off and rest are ______. (Angular retardation is uniform)
A particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is ______.
A particle is performing a uniform circular motion along a circle of radius R. In half the period of revolution, its displacement and distance covered are respectively.
A horizontal circular platform of mass M is rotating at angular velocity ω about a vertical axis passing through its centre. A boy of mass m is standing at the edge of the platform. If the boy comes to the centre of the platform, then the new angular velocity becomes ______.
A wheel is Subjected to uniform angular acceleration about its axis. Initially. its angular velocity is zero. In the first 2 s, it rotates through an angle θ1, in the next 2 s, it rotates through an angle θ2. The ratio of `theta_2/theta_1` is ______.
