Advertisements
Advertisements
प्रश्न
Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.
उत्तर
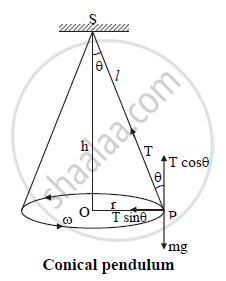
Where, S: rigid support
T : tension in the string
l : length of string
h : height of support from bob
v : velocity of bob
r : radius of horizontal circle
θ: semi-vertical angle
mg : weight of bob
i) Consider a bob of mass m tied to one
end of a string of length ‘l’ and other
the end is fixed to a rigid support.
ii) Let the bob be displaced from its mean
position and whirled around a
horizontal circle of radius ‘r’ with
constant angular velocity ω, then the
bob performs U.C.M.
iii) During the motion, a string is inclined to
the vertical at an angle θ as shown in
the above figure.
iv) In the displaced position P, there are two
forces acting on the bob.
a. The weight mg acting vertically
downwards.
b. The tension T acting upward
along the string.
v) The tension (T) acting in the string can
be resolved into two components:
a. T cos θ acting vertically upwards.
b. T sin θ acting horizontally towards
centre of the circle.
vi) Vertical component T cos θ balances the
weight and horizontal component T sin θ
provides the necessary centripetal force.
∴ T cos θ = mg . ........(1)
T sin θ = `"mv"^2/"r" = "mr"omega^2` ....(2)
vii) Dividing equation (2) by (1),
tan θ = `"v"^2/"rg"` ......(3)
Therefore, the angle made by the string with the vertical is θ = `tan^-1 ("v"^2/"rg")`
Also, from equation (3),
v2 = rg tan θ
∴ v = `sqrt ("rg" tan theta)`
The period, T = `(2pi"r")/"v" = (2pi"r")/sqrt("rg" "tan" theta) = 2pi sqrt ("r"/("g tan" theta))`
It can be seen that r - = l sin θ
T = `2pi sqrt (("l sin" theta)/("g tan" theta)) = 2pi sqrt (("l cos" theta)/"g")`
The period of a conical pendulum is `2pi sqrt (("l cos" theta)/"g")`
APPEARS IN
संबंधित प्रश्न
In U. C. M (Uniform Circular Motion), prove the relation `vec v = vec w xx vec r`, where symbols have their usual meanings.
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Is it possible to have an accelerated motion with a constant speed? Name such type of motion.
Give an example of motion in which speed remains uniform, but the velocity changes.
Differentiate between uniform linear motion and uniform circular motion.
In a uniform circular motion, the speed continuously changes because of the direction of motion changes.
Complete a sentence and explain it.
When an object is in uniform circular motion, its ______ changes at every point.
Which of the following quantity remains constant in a uniform circular motion?
Is it possible to have an accelerated motion with a constant speed? Explain.
Answer the following question.
What is a conical pendulum?
Answer the following question.
Define angular velocity.
Solve the following problem.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
Is the uniform circular motion accelerated? Give reasons for your answer.
The angle subtended by the vector A = `5hat"i" + 3hat"j" + 12hat"k"` with the X-axis is ______.
A disc has mass 'M' and radius 'R'. How much tangential force should be applied to the rim of the disc, so as to rotate with angular velocity 'ω' in time t?
A particle is perfonning uniform circular motion. If 'θ', 'ω', 'α' and ' a' are its angular displacement, angular velocity, angular acceleration, and centripetal acceleration respectively, then which of the following is 'WRONG'?
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
A string of length `l` is fixed at one end and carries a mass 'm' at the other end. The mass is revolving along a horizontal circle of radius 'r' making 'θ' as the semi-vertical angle of cone and `(1/pi)` revolutions per second around the vertical axis through fixed end. The tension in the string is ______.
Statement A: Uniform circular motion is a case of accelerated motion
Statement B: In the third equation of motion we do not have the term time
A body moving along a circular path of radius R with velocity v, has centripetal acceleration a. If its velocity is made equal to 2v. What will be the centripetal acceleration?
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
Earth also moves in circular orbit around sun once every year with on orbital radius of 1.5 × 1011 m. What is the acceleration of earth (or any object on the surface of the earth) towards the centre of the sun? How does this acceleration compare with g = 9.8 m/s2?
A small bead of mass m can move on a smooth circular wire (radius R) under the action of a force F = `"Km"/"r"^2` directed (r = position of bead r from P and K = constant) towards a point P within the circle at a distance R/2 from the centre. The minimum velocity should be ______ m/s of bead at the point of the wire nearest the centre of force (P) so that bead will complete the circle. (Take `"k"/(3"R")` = 8 unit)

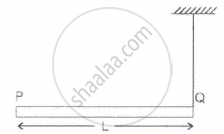
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is ______.
Two bodies of masses 10 kg and 5 kg moving in concentric orbits of radii R and r such that their periods are the same. Then the ratio between their centripetal accelerations is ______.
Why is uniform circular motion said to be accelerated?
