Advertisements
Advertisements
प्रश्न
Answer the following question.
Show that the centripetal force on a particle undergoing uniform circular motion is -mrω2.
उत्तर
- Suppose a particle is performing U.C.M in anticlockwise direction. The co-ordinate axes are chosen as shown in the figure.
Let, A = initial position of the particle which lies on positive X-axis
P = instantaneous position after time t
θ = angle made by radius vector
ω = constant angular speed
`vec"r"` = instantaneous position vector at time t - From the figure,
`vec"r" = hat"i""x" + hat"j""y"`
where, `hat"i" and hat"j"` are unit vectors along X-axis and Y-axis respectively.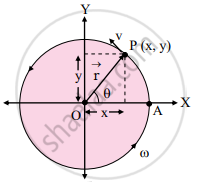
- Also, x = r cos θ and y = r sin θ
∴ `vec"r" = ["r"hat"i"cos theta + "r"hat"j"sin theta]`
But θ = ωt
∴ `vec"r" = ["r"hat"i" cos omega"t" + "r"hat"j" sin omega"t"]` ....(1) - Velocity of the particle is given as rate of change of position vector.
∴ `vec"v" = (vec"dr")/"dt" = "d"/"dt" ["r"hat"i" cos omega"t" + "r" hat"j" sin omega"t"]`
`= "r"["d"/"dt" cos omega"t"]hat"i" + "r"["d"/"dt" sin omega"t"]hat"j"`
∴ `vec"v" = - "r"omega hat"i" sin omega"t" + "r"omega hat"j" cos omega"t"`
∴ `vec"v" = "r"omega (-hat"i" sin omega"t" + hat"j" cos omega"t")` - Further, instantaneous linear acceleration of the particle at instant t is given by,
`vec"a" = (vec"dv")/"dt" = "d"/"dt"["r"omega(- hat"i" sin omega "t" + hat"j" cos omega"t")]`
`= "r"omega ["d"/"dt" (- hat"i" sin omega"t" + hat"j" cos omega "t")]`
`= "r"omega ["d"/"dt" (- sin omega"t")hat"i" + "d"/"dt"(cos omega "t")hat"j"]`
`= "r"omega(-omega hat"i" cos omega"t" - omega hat"j" sin omega "t")`
`= - "r"omega^2(hat"i" cos omega "t" + hat"j" sin omega"t")`
∴ `vec"a" = - omega^2("r"hat"i" cos omega"t" + "r" hat"j" sin omega "t")` ....(2) - From equation (1) and (2),
`vec"a" = - omega^2vec"r"` ....(3)
The negative sign shows that the direction of acceleration is opposite to the direction of the position vector. Equation (3) is the centripetal acceleration. - The magnitude of centripetal acceleration is given by,
a = `omega^2"r"` - The force providing this acceleration should also be in the same direction, hence centripetal.
∴ `vec"F" = "m"vec"a" = - "m"omega^2vec"r"`
This is the expression for the centripetal force on a particle undergoing uniform circular motion. - Magnitude of F = `"m"omega^2"r" = "mv"^2/"r"` = mωv
APPEARS IN
संबंधित प्रश्न
In U. C. M (Uniform Circular Motion), prove the relation `vec v = vec w xx vec r`, where symbols have their usual meanings.
Read the statement below carefully and state, with reason, if it is true or false:
The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
A vehicle is moving on a circular track whose surface is inclined towards the horizon at an angle of 10°. The maximum velocity with which it can move safely is 36 km / hr. Calculate the length of the circular track. [π = 3.142]
Earth moves around the sun with uniform velocity.
State True or False
The earth moves around the sun with a uniform.
In a uniform circular motion, the speed continuously changes because of the direction of motion changes.
A uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
To which side the rule will tilt if the mass m is moved to the mark 10cm ?
Answer the following question.
What is a conical pendulum?
Answer the following question.
Define angular velocity.
Solve the following problem.
A car moves in a circle at a constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Which of the following graph represents uniform motion of a moving particle?
If a particle moves with uniform speed then its tangential acceleration will be ______.
A particle goes round a circular path with uniform speed v. After describing half the circle, what is the change in its centripetal acceleration?
A mass 'm' is tied to one end of a spring and whirled in a horizontal circle with constant angular velocity. The elongation in the spring is 1 cm. If the angular speed is doubled, the elongation in the spring is 6 cm. The original length of the spring is ______.
A cyclist is riding with a speed of 43.2 km/h. As he approaches a circular turn on the road of radius 60 m, he applies brakes and reduces his speed at constant rate of 1.8 ms-2. The magnitude of the net acceleration of the cyclist is ______.
Statement A: Uniform circular motion is a case of accelerated motion
Statement B: In the third equation of motion we do not have the term time
In uniform motion, an object travels equal ______ in ______ interval of time.
The motion of the bus is ______ motion.
If a body is moving in a circle of radius r with a constant speed v, its angular velocity is ______.
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
Earth can be thought of as a sphere of radius 6400 km. Any object (or a person) is performing circular motion around the axis of earth due to earth’s rotation (period 1 day). What is acceleration of object on the surface of the earth (at equator) towards its centre? what is it at latitude θ? How does these accelerations compare with g = 9.8 m/s2?
A small bead of mass m can move on a smooth circular wire (radius R) under the action of a force F = `"Km"/"r"^2` directed (r = position of bead r from P and K = constant) towards a point P within the circle at a distance R/2 from the centre. The minimum velocity should be ______ m/s of bead at the point of the wire nearest the centre of force (P) so that bead will complete the circle. (Take `"k"/(3"R")` = 8 unit)

A particle is performing a uniform circular motion along a circle of radius R. In half the period of revolution, its displacement and distance covered are respectively.
Two bodies of masses 10 kg and 5 kg moving in concentric orbits of radii R and r such that their periods are the same. Then the ratio between their centripetal accelerations is ______.
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions, but of mass `1/4`M is placed gently on the first disc co-axially. The. angular velocity of the system is ______.
A wheel is Subjected to uniform angular acceleration about its axis. Initially. its angular velocity is zero. In the first 2 s, it rotates through an angle θ1, in the next 2 s, it rotates through an angle θ2. The ratio of `theta_2/theta_1` is ______.
Why is uniform circular motion said to be accelerated?
