Advertisements
Advertisements
Question
Answer the following question.
Show that the centripetal force on a particle undergoing uniform circular motion is -mrω2.
Solution
- Suppose a particle is performing U.C.M in anticlockwise direction. The co-ordinate axes are chosen as shown in the figure.
Let, A = initial position of the particle which lies on positive X-axis
P = instantaneous position after time t
θ = angle made by radius vector
ω = constant angular speed
`vec"r"` = instantaneous position vector at time t - From the figure,
`vec"r" = hat"i""x" + hat"j""y"`
where, `hat"i" and hat"j"` are unit vectors along X-axis and Y-axis respectively.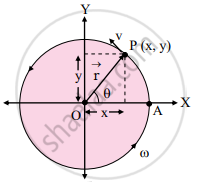
- Also, x = r cos θ and y = r sin θ
∴ `vec"r" = ["r"hat"i"cos theta + "r"hat"j"sin theta]`
But θ = ωt
∴ `vec"r" = ["r"hat"i" cos omega"t" + "r"hat"j" sin omega"t"]` ....(1) - Velocity of the particle is given as rate of change of position vector.
∴ `vec"v" = (vec"dr")/"dt" = "d"/"dt" ["r"hat"i" cos omega"t" + "r" hat"j" sin omega"t"]`
`= "r"["d"/"dt" cos omega"t"]hat"i" + "r"["d"/"dt" sin omega"t"]hat"j"`
∴ `vec"v" = - "r"omega hat"i" sin omega"t" + "r"omega hat"j" cos omega"t"`
∴ `vec"v" = "r"omega (-hat"i" sin omega"t" + hat"j" cos omega"t")` - Further, instantaneous linear acceleration of the particle at instant t is given by,
`vec"a" = (vec"dv")/"dt" = "d"/"dt"["r"omega(- hat"i" sin omega "t" + hat"j" cos omega"t")]`
`= "r"omega ["d"/"dt" (- hat"i" sin omega"t" + hat"j" cos omega "t")]`
`= "r"omega ["d"/"dt" (- sin omega"t")hat"i" + "d"/"dt"(cos omega "t")hat"j"]`
`= "r"omega(-omega hat"i" cos omega"t" - omega hat"j" sin omega "t")`
`= - "r"omega^2(hat"i" cos omega "t" + hat"j" sin omega"t")`
∴ `vec"a" = - omega^2("r"hat"i" cos omega"t" + "r" hat"j" sin omega "t")` ....(2) - From equation (1) and (2),
`vec"a" = - omega^2vec"r"` ....(3)
The negative sign shows that the direction of acceleration is opposite to the direction of the position vector. Equation (3) is the centripetal acceleration. - The magnitude of centripetal acceleration is given by,
a = `omega^2"r"` - The force providing this acceleration should also be in the same direction, hence centripetal.
∴ `vec"F" = "m"vec"a" = - "m"omega^2vec"r"`
This is the expression for the centripetal force on a particle undergoing uniform circular motion. - Magnitude of F = `"m"omega^2"r" = "mv"^2/"r"` = mωv
APPEARS IN
RELATED QUESTIONS
In U. C. M (Uniform Circular Motion), prove the relation `vec v = vec w xx vec r`, where symbols have their usual meanings.
Draw a neat labelled diagram of conical pendulum. State the expression for its periodic time in terms of length.
Read the statement below carefully and state, with reason, if it is true or false:
The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
A particle starts from the origin at t = 0 s with a velocity of 10.0 `hatj "m/s"` and moves in the x-y plane with a constant acceleration of `(8.0 hati + 2.0 hatj) ms^(-2)`.
- At what time is the x-coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?
- What is the speed of the particle at the time?
Is it possible to have an accelerated motion with a constant speed? Explain
A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
Which of the following quantity remains constant in uniform circular motion:
Which of the following remains constant in a uniform circular motion, Speed or Velocity, or both?
Name the force required for uniform circular motion. State its direction.
Answer the following question.
Show that its time period is given by, 2π`sqrt((l cos theta)/("g"))` where l is the length of the string, θ is the angle that the string makes with the vertical, and g is the acceleration due to gravity.
Solve the following problem.
A particle moves in a circle with a constant speed of 15 m/s. The radius of the circle is 2 m. Determine the centripetal acceleration of the particle.
Consider a simple pendulum of length 4 m. Its bob performs a circular motion in horizontal plane with its string making an angle 60° with the vertical. The Period of rotation of the bob is ____________.(Take g = 10 m/s2)
At any instant, the magnitude of the centripetal force on a particle of mass 'm' performing circular motion is given by (ω = angular velocity and v = linear velocity of the particle) ______.
A particle is perfonning uniform circular motion. If 'θ', 'ω', 'α' and ' a' are its angular displacement, angular velocity, angular acceleration, and centripetal acceleration respectively, then which of the following is 'WRONG'?
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
Two particles P and Q are moving in concentric circles of rarui rp and rQ respectively. If their period of revolutions are in ratio 2 : 3, then ratio of their centripetal acceleration is ____________.
A body is said to be in nonuniform motion if it travels ______.
In uniform motion, an object travels equal ______ in ______ interval of time.
The motion of the bus is ______ motion.
Define uniform circular motion and give an example of it. Why is it called accelerated motion?
A cyclist starts from centre O of a circular park of radius 1 km and moves along the path OPRQO as shown figure. If he maintains constant speed of 10 ms–1, what is his acceleration at point R in magnitude and direction?

A disc of radius 5 cm rolls on a horizontal surface with linear velocity v = 1`hat"i"` m/s and angular velocity 50 rad/s. Height of particle from ground on rim of disc which has velocity in vertical direction is ______ cm.
A ceiling fan rotates about its own axis with some angular velocity. When the fan is switched off the angular velocity becomes `(1/4)^"th"` of the original in time 't' and 'n' revolutions are made in that time. The number of revolutions made by the fan during the time interval between switch off and rest are ______. (Angular retardation is uniform)
A particle is performing a uniform circular motion along a circle of radius R. In half the period of revolution, its displacement and distance covered are respectively.
A horizontal circular platform of mass M is rotating at angular velocity ω about a vertical axis passing through its centre. A boy of mass m is standing at the edge of the platform. If the boy comes to the centre of the platform, then the new angular velocity becomes ______.
The acceleration of a point on the rim of a flywheel 1 m in diameter, if it makes 1200 rpm is ______.
