Advertisements
Advertisements
Question
In U. C. M (Uniform Circular Motion), prove the relation `vec v = vec w xx vec r`, where symbols have their usual meanings.
Solution
Analytical method :
Consider a particle revolving in the anticlockwise sense along the circumference of a circle of radius r with centre O as shown.

Let
`vec omega`= angular velocity of the particle
`vec v`= linear velocity of the particle
`vec r`= radius of the particle
In the vector form, the linear dispalcement is
`vec (delta s) = vec (delta theta) times vec r`
Dividing both sides by `delta t` we get
`vec (delta s)/(delta t) = vec (delta theta)/(delta t) times vec r`
`lim_(delta t -> 0) vec (delta s)/(delta t) = lim_(delta t -> 0) vec (delta theta)/(delta t) times vec r`
`therefore vec(dS)/dt = vec(d theta)/(delta t) times vec r`
but
`vec(dS)/dt = vec v` = Linear velocity
`vec(d theta)/(delta t) = vec omega` = angular velocity
`therefore vec v = vec omega times vec r`
APPEARS IN
RELATED QUESTIONS
Read the statement below carefully and state, with reason, if it is true or false:
The velocity vector of a particle at a point is always along the tangent to the path of the particle at that point.
A particle starts from the origin at t = 0 s with a velocity of 10.0 `hatj "m/s"` and moves in the x-y plane with a constant acceleration of `(8.0 hati + 2.0 hatj) ms^(-2)`.
- At what time is the x-coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?
- What is the speed of the particle at the time?
Draw a neat labelled diagram for a particle moving in a circular path with a constant speed. In you diagram show the direction of velocity at any instant.
Give an example of motion in which speed remains uniform, but the velocity changes.
State True or False
The earth moves around the sun with a uniform.
Complete a sentence and explain it.
When an object is in uniform circular motion, its ______ changes at every point.
Which of the following quantity remains constant in a uniform circular motion?
A uniform metre rule of mass 100g is balanced on a fulcrum at mark 40cm by suspending an unknown mass m at the mark 20cm.
To which side the rule will tilt if the mass m is moved to the mark 10cm ?
Which of the following remains constant in a uniform circular motion, Speed or Velocity, or both?
Name the force required for uniform circular motion. State its direction.
Answer the following question.
What is a conical pendulum?
Answer the following question.
Show that its time period is given by, 2π`sqrt((l cos theta)/("g"))` where l is the length of the string, θ is the angle that the string makes with the vertical, and g is the acceleration due to gravity.
Solve the following problem.
A projectile is thrown at an angle of 30° to the horizontal. What should be the range of initial velocity (u) so that its range will be between 40m and 50 m? Assume g = 10 m s-2.
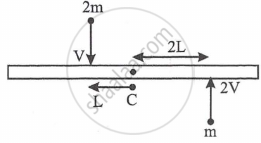
A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and ' 2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity 'w1' then 'w' will be ________.
The ratio of the angular speed of minute hand and hour hand of a watch is ____________.
Consider a simple pendulum of length 4 m. Its bob performs a circular motion in horizontal plane with its string making an angle 60° with the vertical. The Period of rotation of the bob is ____________.(Take g = 10 m/s2)
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
Two particles P and Q are moving in concentric circles of rarui rp and rQ respectively. If their period of revolutions are in ratio 2 : 3, then ratio of their centripetal acceleration is ____________.
The angular speed of the minute hand of a clock in degrees per second is ______.
The given graph represents motion with ______ speed.
A body moves in a uniform circular motion ______.
The motion of the bus is ______ motion.
For a particle performing uniform circular motion, choose the correct statement(s) from the following:
- Magnitude of particle velocity (speed) remains constant.
- Particle velocity remains directed perpendicular to radius vector.
- Direction of acceleration keeps changing as particle moves.
- Angular momentum is constant in magnitude but direction keeps changing.
A ceiling fan rotates about its own axis with some angular velocity. When the fan is switched off the angular velocity becomes `(1/4)^"th"` of the original in time 't' and 'n' revolutions are made in that time. The number of revolutions made by the fan during the time interval between switch off and rest are ______. (Angular retardation is uniform)
A thin uniform circular disc of mass M and radius R is rotating in a horizontal plane about an axis passing through its centre and perpendicular to its plane with an angular velocity ω. Another disc of same dimensions, but of mass `1/4`M is placed gently on the first disc co-axially. The. angular velocity of the system is ______.
The kinetic energy K of a particle moving along a circle of radius R depends on the distance covered s as K = as2, where a is a constant. The force acting on the particle is ______.
