Question

A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and ' 2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity 'w₁' then 'w' will be ________.

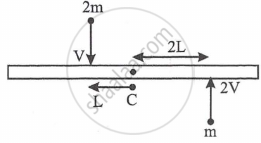
Options

• `"v"/"5L"`

• zero

• `"8v"/"6L"`

• `"11v"/"3L"`

Answer 1

A uniform rod of length '6L' and mass '8 m' is pivoted at its centre 'C'. Two masses 'm' and ' 2m' with speed 2v, v as shown strikes the rod and stick to the rod. Initially the rod is at rest. Due to impact, if it rotates with angular velocity 'w₁' then 'w' will be `underline("v"/"5L")`.

Explanation:

A rod of length 6L and mass am is given in figure,

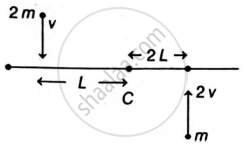
When two masses strike the rod, then angular momentum imparted to rod,

L₁ + L₂ = 2mv(L) + m(2v)(2L)

= 6mvL

Now, after striking of masses to rod the angular momentum of complete rod about the centre C,

L_rod = kω    ...(i)

where, ω = angular velocity of the rod

and l = moment of inertia of the rod.

The moment of inertia of rod

l = `"MI"^2/12 = (8"m"(6"L")^2)/12 = 24 "mL"^2`

∴ M = 8m and I = 6L (given)

Now, moment of inertia of two masses after the striking to I rod

l₁ = 2m(L)² = 2mL²

and l₂ = m(2L)² = 4mL²

∴ The net moment of the inertia about the centre of rod,

l = 24 mL² + 2mL² + 4mL² 

⇒ l = 30mL²

By putting this value in Eq. (i), we get

L_rod = 30 ML² ω

From the law of conservation of angular momentum,

L₁ + L₂ = L_rod

⇒ 6mvL = 30mL² ω 

⇒ `ω = "v"/"5L"`

Hence, the angular velocity of the rod is `"v"/"5L"`.