Advertisements
Advertisements
Question
A particle starts from the origin at t = 0 s with a velocity of 10.0 `hatj "m/s"` and moves in the x-y plane with a constant acceleration of `(8.0 hati + 2.0 hatj) ms^(-2)`.
- At what time is the x-coordinate of the particle 16 m? What is the y-coordinate of the particle at that time?
- What is the speed of the particle at the time?
Advertisements
Solution 1
Velocity of the particle `vecv = 10.0 hatj` m/s
Acceleration of the particle = `veca = (8.0 hati + 2.0 hatj)`
Also
But `veca = (dvecv)/(dt) = 8.0 hati +2.0 hatj`
`(dvecv) = (8.0 hati + 2.0 hatj)dt`
Integrating both sides:
`vecv(t)= 8.0t hati + 2.0t hatj + vecu`
where
`vecu` = velocity vector of the particle at t= 0
`vecv` = velocity vector of the particle at time t
But `vecv = (dvecr)/(dt)`
`dvecr = vecvdt = (8.0t hati + 2.0t hatj + vecu)dt`
Integrating the equations with the conditions: at t = 0; r = 0 andat t = t; r = r
`vecr = vecut + 1/28.0t^2 hati + 1/2xx2.0t^2 hatj`
`=vecut + 4.0t^2 hati + t^2 hatj`
`=(10.0 hatj)t + 4.0t^2 hati + t^2 hatj`
`x hati + y hatj = 4.0t^2 hati + (10t + t^2)hatj`
Since the motion of the particle is confined to the x-y plane, on equating the coefficients of `hati "and" hatj`, we get:
`x = 4t^2`
`t = (x/4)^(1/2)`
And `y = 10t + t^2`
(a) When x = 16 m
`t=(16/4)^(1/2)= 2s`
∴ y = 10 × 2 + (2)2 = 24 m
(b) Velocity of the particle is given by:
`vecv(t) = 8.0t hati + 2.0t hatj + hatu`
at t = 2s
`vecv(t) = 8.0 xx 2 hati + 2.0 xx 2 hatj + 10 hatj`
=`16 hati+ 14 hatj`
∴Speed of the particle
`|vecv| = sqrt((16)^2 + (14)^2)`
`=sqrt(256+196) = sqrt(452)`
`= 21.26 "m/s"`
Solution 2
it is given that `vecr_(t = 0s) = vecv_(0) = 10.0 hatj` m/s and `veca(t) = (8.0 hati + 2.0 hatj) ms^(-2)`
(a) it means `x_0 = 0,u_x = 0, a_x = 8.0` `ms^(-2)` and x = 16 m
Using relation `s = x - x_0 = u_xt+1/2a_xt^2` we have
`16 - 0 = 0 + 1/2 xx 8.0 xx t^2 => t = 2s`
`:.y = y_0 + u_yt+ 1/2a_yt^2 = 0 + 10.0xx2+1/2xx2.0xx(2)^2`
= 20 + 4 = 24 m
(b) Velocity of particle at t= 2 s along x-axis
`v_x = u_x+a_xt=0 + 8.0 xx 2 = 16.0` m/s
and along y-axis `v_y = u_y+a_yt = 10.0 + 2.0 xx 2 = 14.0` m/s
∴Speed of particle at t = 2s
`v= sqrt(v_x^2+v_y^2) = sqrt((16.0)^2+(14.0)^2) = 21.26 ms^(-1)`
APPEARS IN
RELATED QUESTIONS
A stone tied to the end of a string 80 cm long is whirled in a horizontal circle with a constant speed. If the stone makes 14 revolutions in 25 s, what is the magnitude and direction of acceleration of the stone?
Read the statement below carefully and state, with reason, if it is true or false:
The acceleration vector of a particle in uniform circular motion averaged over one cycle is a null vector.
A piece of stone tied at the end of a thread is whirled in a horizontal circle with uniform speed by hand. Answer the following questions:
- Is the velocity of stone uniform or variable?
- Is the acceleration of stone uniform or variable?
- What is the direction of acceleration of stone at any instant?
- Which force provides the centripetal force required for circular motion?
- Name the force and its direction which acts on the hand.
A uniform linear motion is unaccelerated, while a uniform circular motion is an accelerated motion.
Which of the following quantity remains constant in a uniform circular motion?
What is a conical pendulum?
Solve the following problem.
A car moves in a circle at a constant speed of 50 m/s and completes one revolution in 40 s. Determine the magnitude of the acceleration of the car.
Which of the following graph represents uniform motion of a moving particle?
What is meant by uniform circular motion? Give two examples of uniform circular motion.
Certain neutron stars are believed to be rotating at about 1 rev/s. If such a star has a radius of 1.6 km, the acceleration of an object on the equator of the star will be nearly ____________.
Consider a simple pendulum of length 4 m. Its bob performs a circular motion in horizontal plane with its string making an angle 60° with the vertical. The Period of rotation of the bob is ____________.(Take g = 10 m/s2)
A ball of mass 'm' is attached to the free end of an inextensible string of length 'l'. Let 'T' be the tension in the string. The ball is moving in horizontal circular path about the vertical axis. The angular velocity of the ball at any particular instant will be ______.
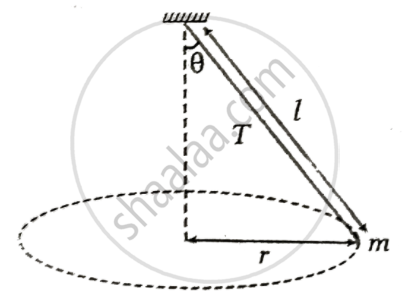
A string of length 'l' fixed at one end carries a mass 'm' at the other end. The string makes `3/pi` revolutions/second around the vertical axis through the fixed end as shown in figure. The tension 'T' in the string is ______.
A stone of mass 3 kg attached at one end of a 2m long string is whirled in horizontal circle. The string makes an angle of 45° with the vertical then the centripetal force acting on the string is ______.
(g = 10 m/s2 , tan 45° = 1)
If a body is moving in a circle of radius r with a constant speed v, its angular velocity is ______.
A wet open umbrella is held upright and is rotated about the handle at a uniform rate of 21 revolutions in 44 s. If the rim of the umbrella is a circle of 1 metre in diameter and the height of the rim above the floor is 1.5 m, the drops of water spun off the rim and hit the floor at a horizontal ______ m from the umbrella.
A rod PQ of mass M and length L is hinged at end P. The rod is kept horizontal by a massless string tied to point Q as shown in figure. When string is cut, the initial angular acceleration of the rod is ______.
A horizontal circular platform of mass M is rotating at angular velocity ω about a vertical axis passing through its centre. A boy of mass m is standing at the edge of the platform. If the boy comes to the centre of the platform, then the new angular velocity becomes ______.
A body of mass m is moving in circle of radius r with a constant speed v. The work done by the centripetal force in moving the body over half the circumference of the circle is ______.
By applying Kepler's third law to the formula for centripetal force, Newton concluded that the force acting on a planet is:
