Advertisements
Advertisements
Question
`hati "and" hatj` are unit vectors along x- and y-axis respectively. What is the magnitude and direction of the vectors `hati+hatj` and `hati-hatj` ? What are the components of a vector `A = 2hati + 3hatj` along the directions of `hati + hatj` and `hati - hatj` ? [You may use graphical method]
Solution
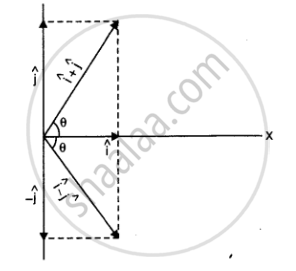
`hati+hatj = sqrt((1)^2 + (1)^2+2xx1xx1xxcos 90^@) = sqrt2` = 1.414 unit
`tan theta = 1/1 = 1 :. theta = 45^@`
So the vector `hati+hatj` makes an angle `45^@` with x-axis
`|hati-hatj| = sqrt((1)^2 +(2)^2 - 2 xx 1xx1xxcos 90^@`
`= sqrt2` = 1.414 units
The vector `hati -hatj` makess an angle `-45^@` with x-axis
Let us now determined the component of `vecA = 2hati+3hatj` in the direction of `hati+hatj`
Let `vecB = hati+hatj`
`vecA.vecB = AB cos theta = (Acostheta)B`
So the component of `vecA` in the direction of `vecB` = `(vecA.vecB)/B`
`=((2hati+3hatj).(hati+hatj))/sqrt((1)^2+(1)^2) = (2hati.hati+2hati.hatj+3hatj.hati+3hatj.hatj)/sqrt2 = 5/sqrt2 units`
Component of `vecA` in the drection of `hati-hatj = ((2hati+3hatj).(hati-hatj))/sqrt2 = -1/sqrt2` units
APPEARS IN
RELATED QUESTIONS
Answer the following question.
Show that `vec"a" = (hat"i" - hat"j")/sqrt2` is a unit vector.
Answer the following question.
If `vec"v"_1 = 3hat"i" + 4hat"j" + hat"k" and vec"v"_2 = hat"i" - hat"j" - hat"k"`, determine the magnitude of `vec"v"_1 + vec"v"_2`.
For `vec"v"_1 = 2hat"i" - 3hat"j" and vec"v"_2 = -6hat"i" + 5hat"j"`, determine the magnitude and direction of `vec"v"_1 + vec"v"_2`.
Find a vector which is parallel to `vec"v" = hat"i" - 2hat"j"` and has a magnitude 10.
Answer the following question.
Show that vectors `vec"a" = 2hat"i" + 5hat"j" - 6hat"k" and vec"b" = hat"i" + 5/2 hat"j" - 3hat"k"` are parallel.
Determine `veca xx vecb`, given `veca = 2hati + 3hatj and vecb = 3hati + 5hatj`.
Walking of a person on the road is an example of
Figure shows the orientation of two vectors u and v in the XY plane.
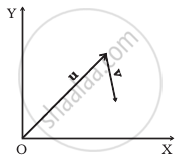
If `u = ahati + bhatj` and `v = phati + qhatj`
which of the following is correct?
The component of a vector r along X-axis will have maximum value if ______.
