Question

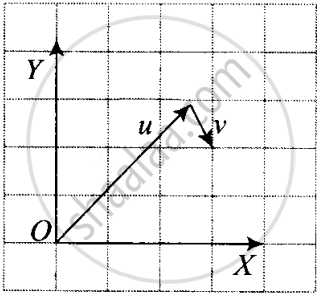
Figure shows the orientation of two vectors u and v in the XY plane.

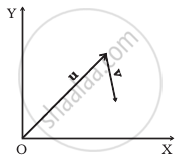
If `u = ahati + bhatj` and `v = phati + qhatj`

which of the following is correct?

Options

• a and p are positive while b and q are negative.

• a, p and b are positive while q is negative.

• a, q and b are positive while p is negative.

• a, b, p and q are all positive.

Answer 1

a, p and b are positive while q is negative.

Explanation:

Resolution of Vector into Components: Consider a vector `vecR` in X - Y plane as shown in the figure. If we draw orthogonal vectors `vecR_x` and `vecR_y` along x and y axes respectively, by the law of vector; addition, `vecR = vecR_x + vecR_y`

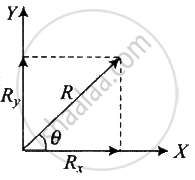
Now as for any vector `vecA = Ahatn, hatn` is the direction of `vecA` so

`vecR_x = hatiR_x` and `vecR_y = hatjR_y`

Thus, `vecR = hatiR_x + hatjR_y` .....(i)

But from figure, `R_x = R cos theta`  ......(ii)

And `R_y = R sin theta`  ......(iii)

Since R and θ are usually known, equations (ii) and (iii) give the magnitude of the components of `vecR` along x- and y-axes respectively.

Here it is worth to note once a vector is resolved into its components, the components themselves can be used to specify the vector as:

(1) The magnitude of the vector `vecR` is obtained by squaring and adding equations (ii) and (iii), i.e.

`R = sqrt(R_x^2 + R_y^2)`

(2) The direction of the vector `vecR` is obtained by dividing equation (iii) by (ii), ie.

`tan theta = (R_y/R_x)` or `theta = tan^-1 (R_y/R_x)`

In such type of problems, we have to resolve the rectangular components according to the diagram.

Clearly from the diagram `vecu = ahati + bhatj`.

As u is in the first quadrant, hence both of its components a and b will be positive and as v is in the fourth quadrant. For `vecv = phati + qhatj`, as it is in positive x-direction and located downward hence x-component p will be positive and y-component q will be negative.