Advertisements
Advertisements
प्रश्न
A barometer is constructed with its tube having radius 1.0 mm. Assume that the surface of mercury in the tube is spherical in shape. If the atmospheric pressure is equal to 76 cm of mercury, what will be the height raised in the barometer tube? The contact angle of mercury with glass = 135° and surface tension of mercury = 0.465 N m−1. Density of mercury = 13600 kg m−3.
उत्तर
Given:
Radius of tube r = 1.0 mm
Atmospheric pressure = 76 cm of Hg
Contact angle of mercury with glass θ = 135°
Surface tension of mercury T = 0.465 N/m
Density of mercury = 13600 kg m−3
Let h be the rise in level in the baromet
\[\text{ h } = \frac{2T\cos\theta}{r\rho g}\]
\[ = \frac{2 \times 465 \times \left( 1/\sqrt{2} \right)}{{10}^{- 3} \times 13600 \times 10} = 0 . 0048 \text{ m}\]
\[ = 0 . 48 \text{ cm}\]
∴ Net rise in level in the barometer tube = H − h
= 76 − 0.48
= 75.52 cm
APPEARS IN
संबंधित प्रश्न
A body weighs 4.0 kg-wt on the surface of the Earth. What will be its weight on the surface of a plant whose mass is `1/8` th of the mass of the Earth and radius half `(1/2)` of that of the Earth?
State any two characteristics of the angle of contact
The contact angle between water and glass is 0°. When water is poured in a glass to the maximum of its capacity, the water surface is convex upward. The angle of contact in such a situation is more than 90°. Explain.
The force of surface tension acts tangentially to the surface whereas the force due to air pressure acts perpendicularly on the surface. How is then the force due to excess pressure inside a bubble balanced by the force due to the surface tension?
When water droplets merge to form a bigger drop
Viscosity is a property of
Find the force exerted by the water on a 2 m2 plane surface of a large stone placed at the bottom of a sea 500 m deep. Does the force depend on the orientation of the surface?
Explain the capillary action.
Derive an expression for capillary rise for a liquid having a concave meniscus.
Define the surface tension of a liquid.
A spherical soap bubble A of radius 2 cm is formed inside another bubble B of radius 4 cm. Show that the radius of a single soap bubble which maintains the same pressure difference as inside the smaller and outside the larger soap bubble is lesser than the radius of both soap bubbles A and B.
The upward force of 105 dyne due to surface tension is balanced by the force due to the weight of the water column and 'h' is the height of water in the capillary. The inner circumference of the capillary is ______.
(surface tension of water = 7 × 10-2 N/m)
The length of a needle floating on water is 2 cm. The additional force due to surface tension required to pull the needle out of water will be (S.T. of water = 7.0 × 10−2 N/m).
The sufrace tension and vapour pressure of water at 20°C is 7.28 × 10–2 Nm–1 and 2.33 × 103 Pa, respectively. What is the radius of the smallest spherical water droplet which can form without evaporating at 20°C?
We have three identical perfectly black plates. The temperatures of first and third plate is T and 3T. What is the temperature of second plate if system is in equilibrium?
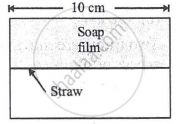
A soap film of surface tension 3 × 10-2 formed in a rectangular frame can support a straw as shown in Fig. If g = 10 ms-12, the mass of the straw is ______.
A spherical liquid drop of radius R is divided into eight equal droplets. If surface tension is T, then the work done in this process will be ______.
A drop of water of radius 8 mm breaks into number of droplets each of radius 1 mm. How many droplets will be formed?
Define angle of contact.
