Advertisements
Advertisements
प्रश्न
Derive Poiseuille’s formula for the volume of a liquid flowing per second through a pipe under streamlined flow.
Advertisements
उत्तर
Consider a liquid flowing steadily through a horizontal capillary tube. Let v = `("V"/"t")` be the volume of the liquid flowing out per second through a capillary tube. It depends on (1) coefficient of viscosity (η) of the liquid, (2) radius of the tube (r), and (3) the pressure gradient `("P"/"l")`.
Then, `"v" ∝ η^"a""r"^"b"("P"/"l")^"c"`
v = `"k"η^"a""r"^"b"("P"/"l")^"c"` .............(1)
where, k is a dimensionless constant.
Therefore, [v] = `"volume"/"time" = ["L"^3"T"^-1], ["dP"/"dx"] = "Pressure"/"distance"`
`["Ml"^-2"T"^-2], [η] = ["M"^-1"T"^-1]` and `["r"] = ["L"]`
Substituting in equation (1)
`["L"^3"T"^-1] = ["ML"^-1"T"^-1]^"a" ["L"]^"b" ["ML"^-2"T"^-2]^"c"`
`"M"^0"L"^3"T"^-1 = "M"^("a" + "c") "L"^(-"a" + "b" - 2"c") "T"^(-"a" - 2"c")`
So, equating the powers of M, L, and T on both sides, we get
a + c = 0, −a + b −2c = 3, and −a −2c = −1
We have three unknowns a, b and c. We have three equations, on solving, we get
a = – 1, b = 4 and c = 1
Therefore, equation (1) becomes,
v = `"k"η^-1"r"^4("P"/"l")^1`
Experimentally, the value of k is shown to be `π/8`, we have
v = `(π"r"^4"P")/(8η"l")`
The above equation is known as Poiseuille’s equation for the flow of liquid through a narrow tube or a capillary tube. This relation holds good for the fluids whose velocities are lesser than the critical velocity (vc).
APPEARS IN
संबंधित प्रश्न
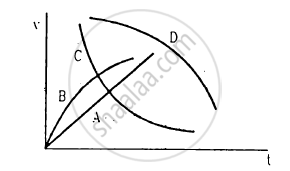
A spherical ball is dropped in a long column of a viscous liquid. The speed of the ball as a function of time may be best represented by the graph
A block of Ag of mass x kg hanging from a string is immersed in a liquid of relative density 0.72. If the relative density of Ag is 10 and tension in the string is 37.12 N then compute the mass of Ag block.
Why two holes are made to empty an oil tin?
From amongst the following curves, which one shows the variation of the velocity v with time t for a small-sized spherical body falling vertically in a long column of a viscous liquid.
In motors, more viscous oil is used in summer than in winter due to ____________.
Clouds float in the air due to ______.
The velocity of a small ball of mass M and density d, when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is `"d"/2` , then the viscous force acting on the ball will be ______.
A solid ball of density ρ1 and radius r falls vertically through a liquid of density ρ2. Assume that the viscous force acting on the ball is F = krv, where k is a constant and v its velocity. What is the terminal velocity of the ball?
The velocity of a small ball of mass 0.3 g and density 8 g/cc when dropped in a container filled with glycerine becomes constant after some time. If the density of glycerine is 1.3 g/cc, then the value of viscous force acting on the ball will be x × 10-4 N, and the value of x is ______.
[use g = 10 m/s2]
An incompressible liquid is flowing through a uniform cross-sectional tube with a velocity 12 cm/ s. If the thickness of liquid layer is 0.8 cm, what is the velocity gradient of that flow of liquid?
