Advertisements
Advertisements
Question
A linear programming problem (LPP) along with the graph of its constraints is shown below.
The corresponding objective function is Z = 18x + 10y, which has to be minimized. The smallest value of the objective function Z is 134 and is obtained at the corner point (3, 8).
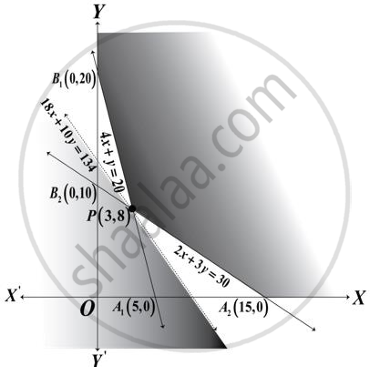
The optimal solution of the above linear programming problem:
Options
Does not exist as the feasible region is unbounded.
Does not exist as the inequality 18x + 10y < 134 does not have any point in common with the feasible region.
Exists as the inequality 18x + 10y > 134 has infinitely many points in common with the feasible region.
Exists as the inequality 18x + 10y < 134 does not have any point in common with the feasible region.
Solution
Exists as the inequality 18x + 10y < 134 does not have any point in common with the feasible region.
Explanation:
Since the inequality Z = 18x + 10y < 134 has no point in common with the feasible region, the minimum value of the objective function Z = 18x + 10y is 134 at P(3, 8).
