Advertisements
Advertisements
Question
A man is 4 times as old as his son. After 16 years he will be only twice as old as his son. Find their present ages.
Solution
Let the present age of the son be x years.
As the man is 4 times as old as his son, the present age of the man will be (4x) years.
After 16 years:
Son's age = (x + 16) years
Man's age = (4x + 16) years
According to the question:
(4x + 16) = 2(x + 16)
or, 4x + 16 = 2 × x + 2 × 16 [On expanding the brackets]
or, 4x + 16 = 2x + 32
or, 4x − 2x = 32 − 16 [Transposing 16 to the R.H.S. and 2x to the L.H.S.]
or, 2x = 16
or, `(2x)/2=16/2` [Dividing both the sides by 2]
or, x = 8
∴ Present age of the son = 8 years
Present age of the man = 4x = 4 × 8
= 32 years
APPEARS IN
RELATED QUESTIONS
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
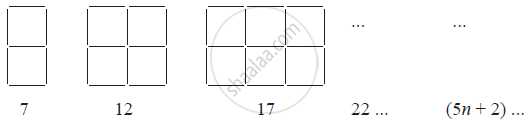
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind −
Write down the following in the product form: 10a3b3c3
One out of two numbers is thrice the other. If their sum is 124, find the numbers.
The additive inverse of an integer x is 2x.
The side length of the top of square table is x. The expression for perimeter is ______.
The speed of car is 55 km/hrs. The distance covered in y hours is ______.
The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 5 natural numbers.
The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 11 natural numbers.
The sum of squares of first n natural numbers is given by `1/6n(n + 1)(2n + 1)` or `1/6(2n^3 + 3n^2 + n)`. Find the sum of squares of the first 10 natural numbers.
If 
= `3/4x - 2` and 
= x + 6, then find the value of:
2
– `3/2`
