Advertisements
Advertisements
Question
Mrs. Goel is 27 years older than her daughter Rekha. After 8 years she will be twice as old as Rekha. Find their present ages.
Solution
Let the present age of Rekha be x years.
As Mrs. Goel is 27 years older than Rekha, the present age of Mrs. Goel will be (x + 27) years.
After 8 years:
Rekha's age = (x + 8) years
Mrs. Goel's age = (x + 27 + 8)
= (x + 35) years
According to the question:
(x + 35) = 2(x + 8)
or, x + 35 = 2 × x + 2 × 8 [On expanding the brackets]
or, x + 35 = 2x + 16
or, 35 − 16 = 2x − x [Transposing 16 to the L.H.S. and x to the R.H.S.]
or, x = 19
∴ Present age of Rekha = 19 years
Present age of Mrs. Goel = x + 27
= 19 + 27
= 46 years
APPEARS IN
RELATED QUESTIONS
Observe the patterns of digits made from line segments of equal length. You will find such segmented digits on the display of electronic watches or calculators.
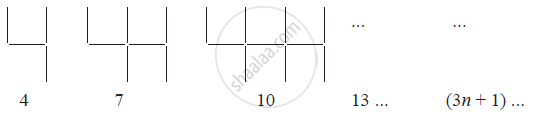
If the number of digits formed is taken to be n, the number of segments required to form n digits is given by the algebraic expression appearing on the right of each pattern.
How many segments are required to form 5, 10, 100 digits of the kind −

If 11 is subtracted from 4 times a number, the result is 89. Find the number.
The sum of three consecutive natural numbers is 114. Find the numbers.
Find two numbers such that one of them exceeds the other by 18 and their sum is 92.
If m is a whole number, then 2 m denotes a multiple of 2.
The diameter of a circle is a line which joins two points on the circle and also passed through the centre of the circle. (In the adjoining figure AB is a diameter of the circle; C is its centre.) Express the diameter of the circle (d) in terms of its radius (r).

To find sum of three numbers 14, 27 and 13, we can have two ways:
- We may first add 14 and 27 to get 41 and then add 13 to it to get the total sum 54 or
- We may add 27 and 13 to get 40 and then add 14 to get the sum 54. Thus, (14 + 27) + 13 = 14 + (27 + 13)
This can be done for any three numbers. This property is known as the associativity of addition of numbers. Express this property which we have already studied in the chapter on whole numbers, in a general way, by using variables a, b and c.
The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 5 natural numbers.
The sum of first n natural numbers is given by `1/2n^2 + 1/2n`. Find the sum of first 11 natural numbers.
Write an expression for the sum of 1 and twice a number n. If you let n be any odd number, will the result always be an odd number?
