Advertisements
Advertisements
Question
A measuring jar of internal diameter 10 cm is partially filled with water. Four equal spherical balls of diameter 2 cm each are dropped in it and they sink down in water completely. What will be the change in the level of water in the jar?
Solution
Given that,
Diameter of jar = 10cm
Radius of jar = 5cm
Let the level of water raised by ‘h’
Diameter of spherical ball = 2cm
Radius of the ball =1cm
Volume of jar = 4(Volume of spherical)
⇒ `πr_1^2h=4(4/3πr_2^3)`
⇒`r_1^2h=4xx4/3r_2^3`
⇒`r_1^2h=4xx4/3xx1xx1xx1`
⇒`h=(4xx4xx1)/(3xx5xx5)`
⇒`h=16/75cm.`
∴ Height of water in jar`16/75`cm.
APPEARS IN
RELATED QUESTIONS
The diameter of the moon is approximately one-fourth of the diameter of the earth. What fraction of the volume of the earth is the volume of the moon?
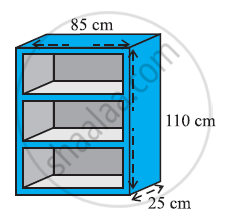
A wooden bookshelf has external dimensions as follows: Height = 110 cm, Depth = 25 cm, Breadth = 85 cm (see the given figure). The thickness of the plank is 5 cm everywhere. The external faces are to be polished and the inner faces are to be painted. If the rate of polishing is 20 paise per cm2 and the rate of painting is 10 paise per cm2, find the total expenses required for polishing and painting the surface of the bookshelf.
The diameter of a sphere is decreased by 25%. By what per cent does its curved surface area decrease?
Find the volume of a sphere whose diameter is 3.5 dm .
A spherical ball of lead 3 cm in diameter is melted and recast into three spherical balls. If the diameters of two balls be `3/2`cm and 2 cm, find the diameter of the third ball.
A cone, a hemisphere and a cylinder stand on equal bases and have the same height. Show that their volumes are in the ratio 1 : 2 : 3.
Volume of a hemisphere is 18000 π cubic cm. Find its diameter.
A cone is 8.4 cm high and the radius of its base is 2.1 cm. It is melted and recast into a sphere. The radius of the sphere is ______.
The number of planks of dimensions (4 m × 50 cm × 20 cm) that can be stored in a pit which is 16 m long, 12 m wide and 4 m deep is ______.
The volume of a sphere is equal to two-third of the volume of a cylinder whose height and diameter are equal to the diameter of the sphere.
