Question

A metal sphere of radius 1 mm and mass 50 mg falls vertically in glycerine. Find (a) the viscous force exerted by the glycerine on the sphere when the speed of the sphere is 1 cm s⁻¹, (b) the hydrostatic force exerted by the glycerine on the sphere and (c) the terminal velocity with which the sphere will move down without acceleration. Density of glycerine = 1260 kg m⁻³ and its coefficient of viscosity at room temperature = 8.0 poise. 

Answer 1

Given:
Radius of metallic sphere r = 1 mm = 10⁻³ m
Speed of the sphere v = 10⁻² m/s
Coefficient of viscosity η = 8 poise = 0.8 decapoise
Mass m = 50 mg = 50 × 10⁻³ kg
Density of glycerin σ = 1260 kg/m³

(a) Viscous force exerted by glycerine on the sphere F = 6πηrv
⇒ F= 6 × (3.14) × (0.8) × 10⁻³ × (10⁻²)
     = 1.50 × 10⁻⁴ N
(b) Let V be the volume of the sphere. 
Hydrostatic force exerted by glycerin on the sphere 

\[F' = V\sigma g\]

\[\Rightarrow F' = \frac{4}{3}\pi r^2 \sigma g\]

\[= \left( \frac{4}{3} \right) \times \left( 3 . 14 \right) \times \left( {10}^{- 6} \right) \times 1260 \times 10\]

\[ = 5 . 275 \times {10}^{- 5} \text{N}\]

(c) Let the terminal velocity of the sphere be v'.
The forces acting on the drops are
(i) The weight mg acting downwards
(ii) The force of buoyance, i.e.,  \[\frac{4}{3}\pi r^3 \sigma g\]  acting upwards 

(iii) The force of viscosity, i.e., 6πηrv' acting upwards
From the free body diagram: 

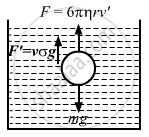
\[6\pi\eta r v' + \frac{4}{3}\pi r^3 \sigma g = \text{ mg}\]

\[ \Rightarrow v = \frac{\text{ mg }- \frac{4}{3}\pi r^2 \sigma g}{6\pi\eta r}\]

\[ = \frac{50 \times {10}^{- 3} - \frac{4}{3} \times 3 . 14 \times {10}^{- 6} \times 1260 \times 10}{6 \times 3 . 14 \times 0 . 8 \times {10}^{- 3}}\]

\[ = \frac{500 - \frac{4}{3} \times 3 . 14 \times {10}^{- 3} \times 1260 \times 10}{6 \times 3 . 14 \times 0 . 8}\]

\[ = 2 . 3 \text{ cm/s }\]