Advertisements
Advertisements
Question
A metal wire, when bent in the form of a square of largest area, encloses an area of 484 cm2. Find the length of the wire. If the same wire is bent to the largest circle, find:
(i) radius of the circle formed.
(ii) area of the circle.
Solution
Area of the square made wire = 484 cm2
∴ Length (side) = `sqrt"Area"=sqrt484` = 22 cm
(i) Perimeter of wire = 4 × Side
= 4 × 22 = 88 cm
∴ Circumference of circular wire = 88 cm
∴ Radius (r) = `"C"/(2π)=(88xx7)/(2xx22)"cm"` = 14 cm
(ii) ∴ Area of the circle = πr2
= `22/7xx14xx14` = 616 cm2
APPEARS IN
RELATED QUESTIONS
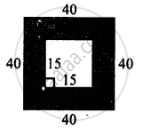
In the figure given below, find the area of shaded region: (All measurements are in cm)
One side of a parallelogram is 18 cm and its area is 153 cm2. Find the distance of the given side from its opposite side.
The area of a rhombus is 84 cm2 and its perimeter is 56 cm. Find its height.
Find the area of a triangle whose base is 30 cm and the height is 18 cm.
Find the area of an equilateral triangle whose each side is 16 cm. (Take `sqrt3`= 1.73)
Find the area of an isosceles triangle whose base is 16 cm and the length of each of the equal sides is 10 cm.
The area of an equilateral triangle is (`64xxsqrt3`) cm2. Find the length of each side of the triangle.
The sides of a triangle are in the ratio 15 : 13 : 14 and its perimeter is 168 cm. Find the area of the triangle.
The ratio between the radius of two circles is 5 : 7. Find the ratio between their:
(i) circumference
(ii) areas
The ratio between the areas of two circles is 16 : 9. Find the ratio between their :
(i) radius
(ii) diameters
(iii) circumference
