Advertisements
Advertisements
Question
A metallic rod of length ‘l’ is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
Solution
Suppose the length of the rod is greater than the radius of the circle and rod rotates anticlockwise and suppose the direction of electrons in the rod at any instant be along +y-direction.
Suppose the direction of the magnetic field is along +z-direction.
Then, using Lorentz law, we get the following:
`vecF = -e (vecv xx vecB)`
`=> vecF = -e(vhatj xx Bhatk)`
`=> hatF = -evBhati`
Thus, the direction of force on the electrons is along −x axis.
Thus, the electrons will move towards the center i.e., the fixed end of the rod. This movement of electrons will result in current and hence it will produce emf in the rod between the fixed end and the point touching the ring.
Let θ be the angle between the rod and radius of the circle at any time t.
Then, area swept by the rod inside the circle `= 1/2 πr^2θ`
Inducced emf ` = B xx d/dt (1/2πr^2θ) =1/2πr^2B (dθ)/dt = 1/2πr^2Bω = 1/2πr^2B (2πv) = π^2r^2Bv`
NOTE: There will be an induced emf between the two ends of the rods also.
RELATED QUESTIONS
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
Figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mΩ. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s−1 in the direction shown. Give the polarity and magnitude of the induced emf.
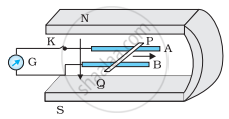
(b) Is there an excess charge built up at the ends of the rods when K is open? What if K is closed?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed = (12 cm s−1) when K is closed? How much power is required when K is open?
(f) How much power is dissipated as heat in the closed circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth's magnetic field is 5 × 10–4 T and the angle of dip is 30°.
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
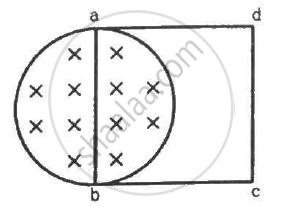
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
Two identical coaxial coils P and Q carrying equal amount of current in the same direction are brought nearer. The current in ______.
