Advertisements
Advertisements
Question
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
Solution

where
E1, E2 = Emf of two cells
r1, r2 = Internal resistances of cell
I1, I2 = Current due to the two cells
Terminal potential difference across the first cell is
V = E1 − I1r1
`=>I_1=(E_1-V)/r_1`
For the second cell, terminal potential difference will be equal to that across the first cell. So,
V = E2 − I2r2
`⇒I_2=(E_2−V)/r_2`
Let E be effective emf and r is effective internal resistance. Let I be the current flowing through the cell.
I=I1+I2
`⇒I=(E1−V)/r_1+(E2−V)/r_2`
`⇒Ir_1r_2=E_1r_2+E_1r_1−(r_1+r_2)V`
`=>V=(E_1r_2+E_2r_1)/(r_1+r_2)−(Ir_1r_2)/(r_1+r_2)`
Comparing the equation with V=E−Ir, we get
`E=(E_1r_2+E_2r_1)/(r_1+r_2)`
`r=(r_1r_2)/(r_1+r_2)`
APPEARS IN
RELATED QUESTIONS
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth's magnetic field is 5 × 10–4 T and the angle of dip is 30°.
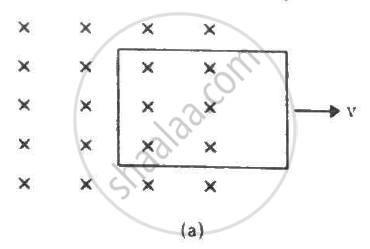
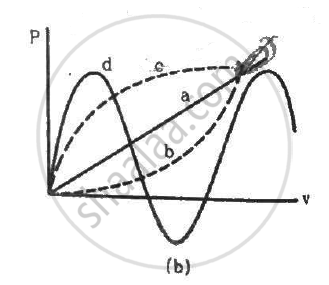
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
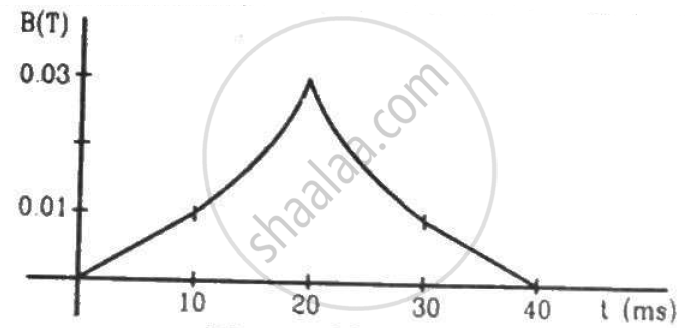
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
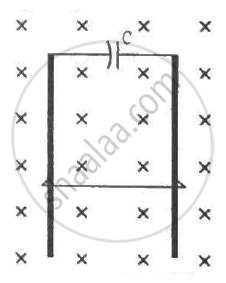
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
