Advertisements
Advertisements
Question
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
Solution
According to the principle of homogeneity of dimensions, the dimensions of each term on both the sides of a correct equation must be the same.
Now,
ϕ = at2 + bt + c
(a) The dimensions of the quantities at2, bt, c and ϕ must be the same.
Thus, the units of the quantities are as follows:-
\[a = \left( \frac{\phi}{t^2} \right) = \left[ \frac{\phi/t}{t} \right] = \frac{Volt}{s}\]
\[b = \left[ \frac{\phi}{t} \right] = \text{Volt}\]
\[c = \left[ \phi \right] = \text{Weber}\]
(b) The emf is written as:-
\[E = \frac{d\phi}{dt}=2at+b=2\times0.2\times2+0.4..........\left(\because a=0.2, b=0.4\text{ and }c=0.6\right)\]
On substituting t = 2 s, we get
E = 0.8 + 0.4
= 1.2 V
APPEARS IN
RELATED QUESTIONS
State Lenz’s Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
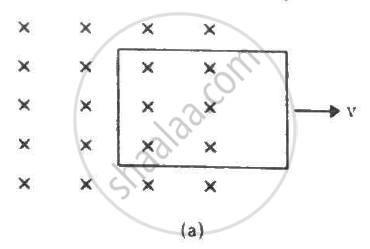
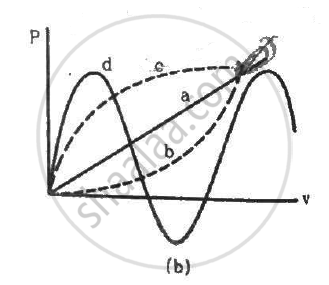
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
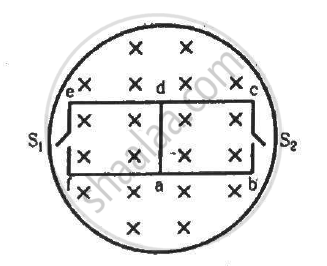
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
A closed coil having 100 turns is rotated in a uniform magnetic field B = 4.0 × 10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25 cm2 and its resistance is 4.0 Ω. Find (a) the average emf developed in half a turn from a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h−1? The vertical component of earth's magnetic field is 0.2 × 10−4 T and the rails are separated by 1 m.
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
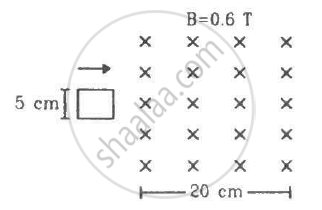
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
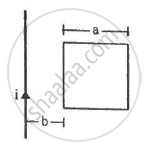
Figure shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i = i0 sin ωt. Find (a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to \[\frac{20\pi}{\omega}.\]
The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
An induced e.m.f. is produced when a magnet is plunged into a coil. The strength of the induced e.m.f. is independent of ______.
Two identical coaxial coils P and Q carrying equal amount of current in the same direction are brought nearer. The current in ______.
