Advertisements
Advertisements
Question
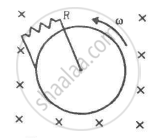
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
Solution
Given:-
Magnetic field perpendicular to the disc, B = 0.40 T
Angular speed, ω = 10 rad/s
Resistance, R = 10 Ω
Radius of the disc, r = 5 cm = 0.5 m
Let us consider a rod of length 0.05 m fixed at the centre of the disc and rotating with the same ω.
Now,
\[v = \frac{l}{2} \times \omega = \frac{0 . 05}{2} \times 10\]
\[e = Blv\]
\[ = 0 . 40 \times 0 . 05 \times \frac{0 . 05}{2} \times 10\]
\[ = 5 \times {10}^{- 3} V\]
\[i = \frac{e}{R}\]
\[ = \frac{5 \times {10}^{- 3}}{10} = 0 . 5 mA\]
As the disc is rotating in the anti-clockwise direction, the emf induced in the disc is such that the centre is at the higher potential and the periphery is at the lower potential. Thus, the current leaves from the centre.
APPEARS IN
RELATED QUESTIONS
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is __________________ .
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
A square-shaped copper coil has edges of length 50 cm and contains 50 turns. It is placed perpendicular to a 1.0 T magnetic field. It is removed from the magnetic field in 0.25 s and restored in its original place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
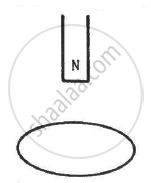
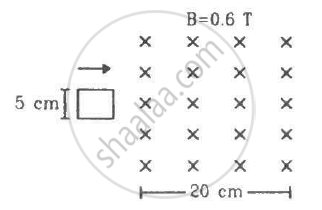
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
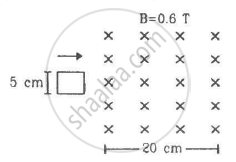
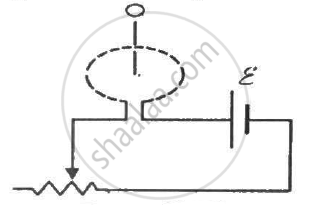
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
The magnetic field in a region is given by \[\overrightarrow{B} = \overrightarrow{k} \frac{B_0}{L}y\] where L is a fixed length. A conducting rod of length L lies along the Y-axis between the origin and the point (0, L, 0). If the rod moves with a velocity v = v0 \[\overrightarrow{i},\] find the emf induced between the ends of the rod.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
Plot a graph showing variation of induced e.m.f. with the rate of change of current flowing through a coil.
Two identical coaxial coils P and Q carrying equal amount of current in the same direction are brought nearer. The current in ______.
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
