Advertisements
Advertisements
Question
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
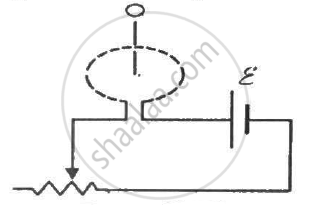
Solution
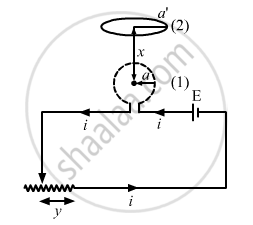
The magnetic field due to coil 1 at the centre of coil 2 is given by
\[B = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\]
The flux linked with coil 2 is given by
\[\phi = B . A' = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\pi a '^2\]
Now, let y be the distance of the sliding contact from its left end.
Given:-
\[v = \frac{dy}{dt}\]
Total resistance of the rheostat = R
When the distance of the sliding contact from the left end is y, the resistance of the rheostat (R') is given by
\[R' = \frac{R}{L}y\]
The current in the coil is the function of distance y travelled by the sliding contact of the rheostat. It is given by
\[i = \frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
The magnitude of the emf induced can be calculated as:-
\[e = \frac{d\phi}{dt} = \frac{\mu_0 N a^2 a '^2 \pi}{2 ( a^2 + x^2 )^{3/2}}\frac{di}{dt}\]
\[\Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\frac{d}{dt}\frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\left[ \epsilon\frac{\left( - \frac{R}{L}v \right)}{\left( \frac{R}{L}y + r \right)^2} \right]\]
(a) For y = L,
\[e = \frac{\mu_0 N \pi a^2 a '^2 \epsilon Rv}{2L ( a^2 + x^2 )^{3/2} (R + r )^2}\]
(b) For y = L/2,
\[\frac{R}{L}y = \frac{R}{2}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2L( a^2 + x^2 )^{3/2}}\frac{\epsilon Rv}{\left( \frac{R}{2} + r \right)^2}\]
APPEARS IN
RELATED QUESTIONS
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
What is motional emf? State any two factors on which it depends.
State Lenz’s Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
Consider the following statements:-
(A) An emf can be induced by moving a conductor in a magnetic field.
(B) An emf can be induced by changing the magnetic field.
An LR circuit with a battery is connected at t = 0. Which of the following quantities is not zero just after the connection?
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
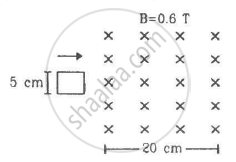
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
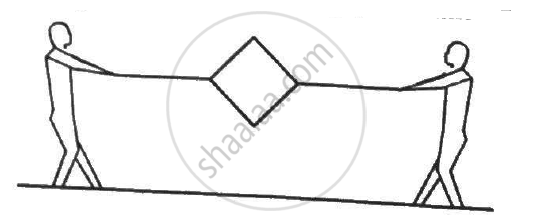
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
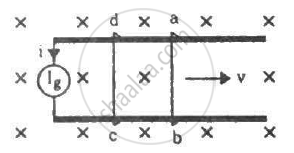
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.
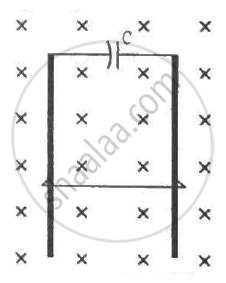
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
Plot a graph showing variation of induced e.m.f. with the rate of change of current flowing through a coil.
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
