Advertisements
Advertisements
प्रश्न
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
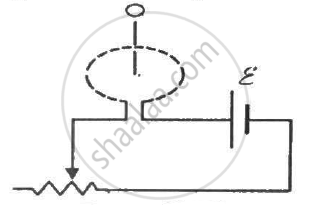
उत्तर
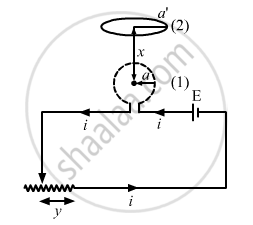
The magnetic field due to coil 1 at the centre of coil 2 is given by
\[B = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\]
The flux linked with coil 2 is given by
\[\phi = B . A' = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\pi a '^2\]
Now, let y be the distance of the sliding contact from its left end.
Given:-
\[v = \frac{dy}{dt}\]
Total resistance of the rheostat = R
When the distance of the sliding contact from the left end is y, the resistance of the rheostat (R') is given by
\[R' = \frac{R}{L}y\]
The current in the coil is the function of distance y travelled by the sliding contact of the rheostat. It is given by
\[i = \frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
The magnitude of the emf induced can be calculated as:-
\[e = \frac{d\phi}{dt} = \frac{\mu_0 N a^2 a '^2 \pi}{2 ( a^2 + x^2 )^{3/2}}\frac{di}{dt}\]
\[\Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\frac{d}{dt}\frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\left[ \epsilon\frac{\left( - \frac{R}{L}v \right)}{\left( \frac{R}{L}y + r \right)^2} \right]\]
(a) For y = L,
\[e = \frac{\mu_0 N \pi a^2 a '^2 \epsilon Rv}{2L ( a^2 + x^2 )^{3/2} (R + r )^2}\]
(b) For y = L/2,
\[\frac{R}{L}y = \frac{R}{2}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2L( a^2 + x^2 )^{3/2}}\frac{\epsilon Rv}{\left( \frac{R}{2} + r \right)^2}\]
APPEARS IN
संबंधित प्रश्न
The current flowing through an inductor of self-inductance L is continuously increasing. Plot a graph showing the variation of
Induced emf versus dI/dt
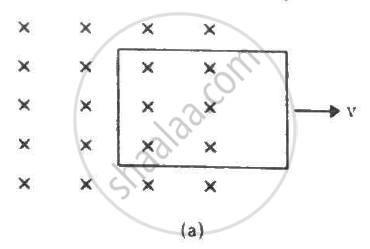
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

What is motional emf? State any two factors on which it depends.
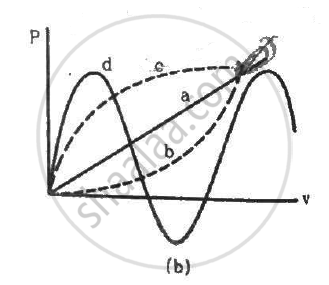
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
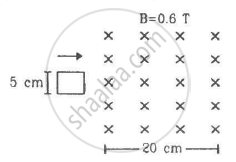
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h−1? The vertical component of earth's magnetic field is 0.2 × 10−4 T and the rails are separated by 1 m.
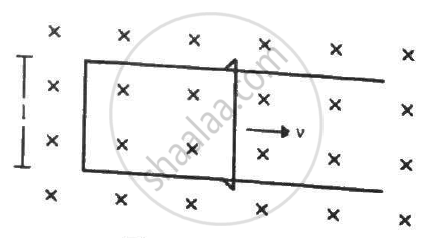
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
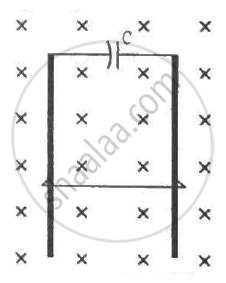
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
Plot a graph showing variation of induced e.m.f. with the rate of change of current flowing through a coil.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
