Advertisements
Advertisements
प्रश्न
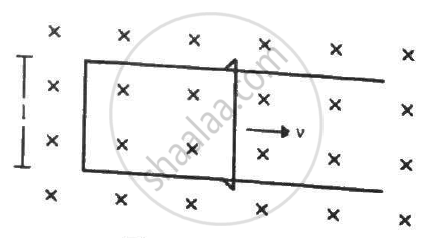
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
उत्तर
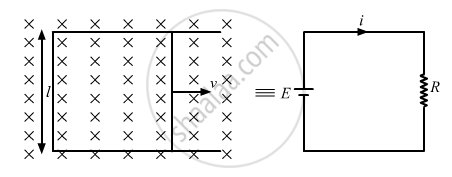
The induced emf is given by
e = Bvl
Total resistance, R = r × Total length of the wire
Because the length of the movable wire is l and the distance travelled by the movable wire in time t is vt, the total length of the loop is 2 (l + vt).
∴ e = i × 2r (l + vt)
Bvl = 2ri (l + vt)
\[\Rightarrow i = \frac{Bvl}{2r(l + vt)}\]
APPEARS IN
संबंधित प्रश्न
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
A conducting loop is placed in a uniform magnetic field with its plane perpendicular to the field. An emf is induced in the loop if ___________.
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
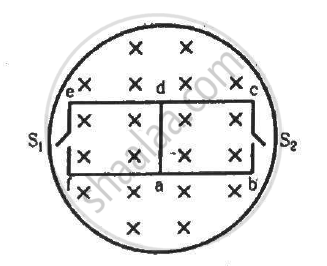
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
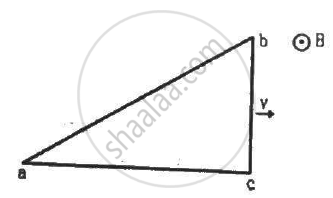
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
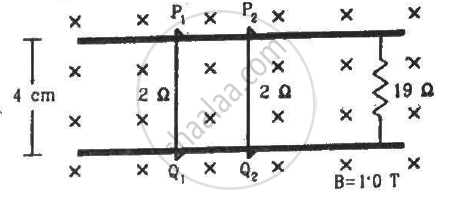
Consider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5 cm s−1. Find the electric current in the 19 Ω resistor if (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
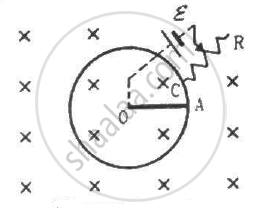
Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. A battery of emf ε and a variable resistance R are connected between O and C. Neglect the resistance of the connecting wires. Let θ be the angle made by the rod from the horizontal position (show in the figure), measured in the clockwise direction. During the part of the motion 0 < θ < π/4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
Plot a graph showing variation of induced e.m.f. with the rate of change of current flowing through a coil.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
When the rate of change oic current is unity, the induced emf is equal to ______.
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magnetic field is reduced from its initial value of 0.3 T at the rate of 0.02 T s-1 If the cut is joined and loop has a resistance of 1.6 Ω, then how much power is dissipated by the loop as heat?
