Advertisements
Advertisements
प्रश्न
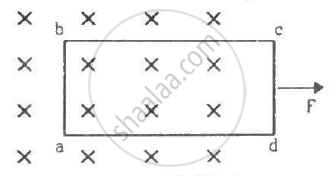
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
उत्तर
Given:-
Total resistance of the frame, R = 2.0 Ω
Magnetic field, B = 0.020 T
Dimensions of the frame:-
Length, l = 32 cm = 0.32 m
Breadth, b = 8 cm = 0.08 m
(a) Let the velocity of the frame be v.
The emf induced in the rectangular frame is given by
e = Blv
Current in the coil,
\[i = \frac{Blv}{R}\]
The magnetic force on the rectangular frame is given by
F = ilB = 3.2 × 10−5 N
On putting the value of i, we get
\[\frac{B^2 l^2 v}{R} = 3 . 2 \times {10}^{- 5} \]
\[ \Rightarrow \frac{(0 . 020 )^2 \times (0 . 08 )^2 \times v}{2} = 3 . 2 \times {10}^{- 5} \]
\[ \Rightarrow v = \frac{3 . 2 \times {10}^{- 5}}{6 . 4 \times {10}^{- 3} \times 4 \times {10}^{- 4}}\]
\[ = 25 m/s\]
(b) Emf induced in the loop, e = vBl
⇒ e = 25 × 0.02 × 0.08
= 4 × 10−2 V
(c) Resistance per unit length is given by
`r=2/0.8`
Ratio of the resistance of part,
\[\frac{ad}{cb} = \frac{2 \times 0 . 72}{0 . 8} = 1 . 8 \Omega\]
\[V_{ab} = iR = \frac{Blv}{2} \times 1 . 8\]
\[ = \frac{0 . 2 \times 0 . 08 \times 25 \times 1 . 8}{2}\]
\[ = 0 . 036 V = 3 . 6 \times {10}^{- 2} V\]
(d) Resistance of cd:-
\[R_{cd} = \frac{2 \times 0 . 8}{0 . 8} = 0 . 2 \Omega\]
\[V = i R_{cd} = \frac{2 \times 0 . 08 \times 25 \times 0 . 2}{2}\]
\[= 4 \times {10}^{- 3} V\]
APPEARS IN
संबंधित प्रश्न
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is ______________ .
Consider the following statements:-
(A) An emf can be induced by moving a conductor in a magnetic field.
(B) An emf can be induced by changing the magnetic field.
Consider the situation shown in figure. The wire AB is slid on the fixed rails with a constant velocity. If the wire AB is replaced by a semicircular wire, the magnitude of the induced current will _____________ .

A conducting loop is placed in a uniform magnetic field with its plane perpendicular to the field. An emf is induced in the loop if ___________.
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
A metallic metre stick moves with a velocity of 2 m s−1 in a direction perpendicular to its length and perpendicular to a uniform magnetic field of magnitude 0.2 T. Find the emf induced between the ends of the stick.
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
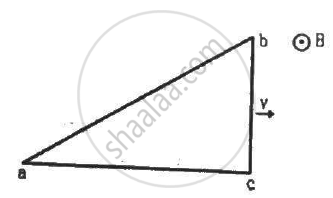
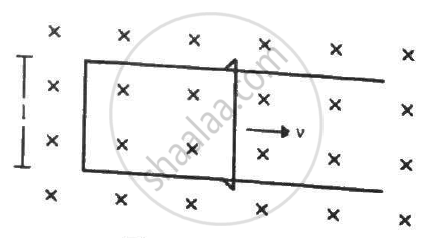
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
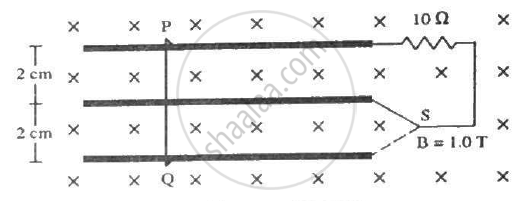
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s−1. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
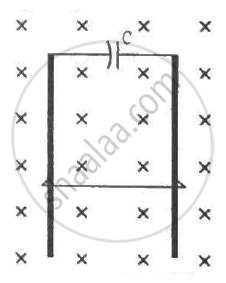
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
The current in an ideal, long solenoid is varied at a uniform rate of 0.01 As−1. The solenoid has 2000 turns/m and its radius is 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 2.0 seconds. (b) Find the electric field induced at a point on the circumference of the circle. (c) Find the electric field induced at a point outside the solenoid at a distance 8.0 cm from its axis.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magnetic field is reduced from its initial value of 0.3 T at the rate of 0.02 T s-1 If the cut is joined and loop has a resistance of 1.6 Ω, then how much power is dissipated by the loop as heat?
