Advertisements
Advertisements
प्रश्न
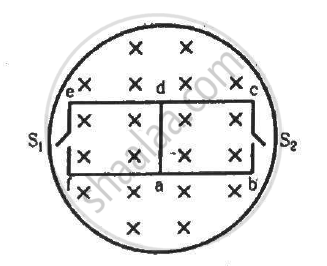
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
उत्तर
(a) When switch S1 is closed and switch S2 is open:-
Rate of change of the magnetic field = 20 mT/s = \[2 \times {10}^{- 4} T/s\]
Net resistance of the coil adef, R = 4 × 4 = 16 Ω
Area of the coil adef = (10−2 )−2 = 10−4 m2
The emf induced is given by
\[e = \frac{d\phi}{dt} = A . \frac{dB}{dt}\]
= 10−4 × 2 × 10−2
= 2 × 10−6 V
The current through the wire ad is given by
\[i= \frac{e}{R} = \frac{2 \times {10}^{- 6}}{16}\]
= 1.25 × 10−7 A along ad
(b) When switch S2 is closed and switch S1 is open:-
Net resistance of the coil abcd, R = 16 Ω
The induced emf is given by
\[e = A \times \frac{dB}{dt} = 2 \times {10}^{- 6} V\]
The current through wire ad is given by
\[i = \frac{20 \times {10}^{- 6}}{16} = 1 . 25 \times {10}^{- 7} A \] along da
(c) When both S1 and S2 are open, no current is passed, as the circuit is open. Thus, i = 0.
(d) When both S1 and S2 are closed, the circuit forms a balanced a Wheatstone bridge and no current flows along ad. Thus, i = 0.
APPEARS IN
संबंधित प्रश्न
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
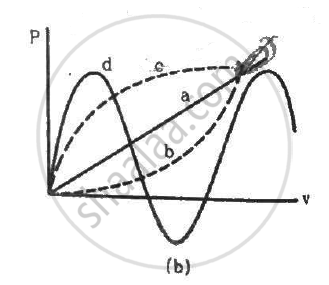
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
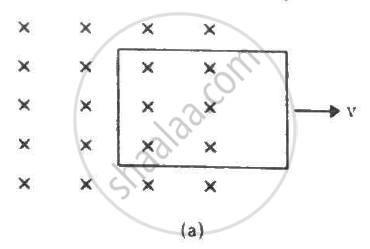
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
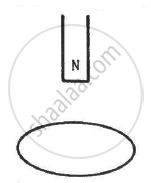
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
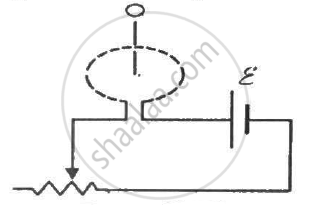
A closed coil having 100 turns is rotated in a uniform magnetic field B = 4.0 × 10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25 cm2 and its resistance is 4.0 Ω. Find (a) the average emf developed in half a turn from a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
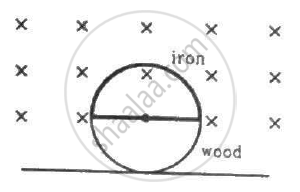
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
A 10 m wide spacecraft moves through the interstellar space at a speed 3 × 107 m s−1. A magnetic field B = 3 × 10−10 T exists in the space in a direction perpendicular to the plane of motion. Treating the spacecraft as a conductor, calculate the emf induced across its width.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
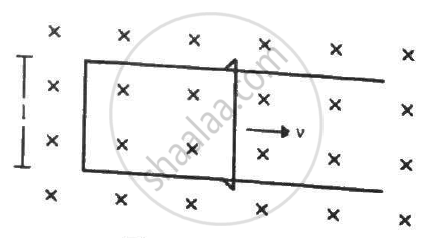
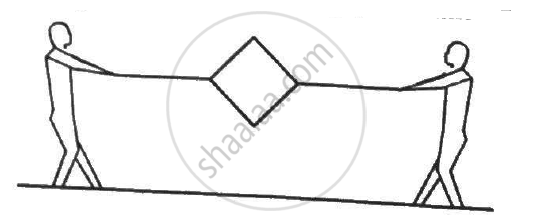
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) What would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a function of time. (g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
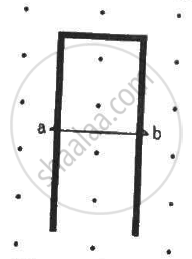
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
A small flat search coil of area 5cm2 with 140 closely wound turns is placed between the poles of a powerful magnet producing magnetic field 0.09T and then quickly removed out of the field region. Calculate:
(a) Change of magnetic flux through the coil, and
(b) emf induced in the coil.
