Advertisements
Advertisements
प्रश्न
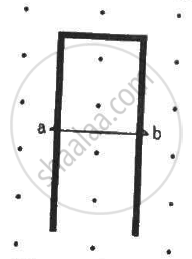
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) What would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a function of time. (g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
उत्तर
(a) When the speed of the wire is v, the emf developed in the loop is, e = Blv.
(b) Magnitude of the induced current in the wire, I = \[\frac{Blv}{R}\]
As wire is moving the magnetic flux passing through the loop is increasing with time. Therefore, the direction of the current should be as such to oppose the change in magnetic flux. Therefore in order to induce the current in anticlockwise direction the current flows from b to a
(c) Due to motion of the wire in the magnetic field there is a force in upward direction (perpendicular to the wire).
The magnitude of the force on the wire carrying current i is given by F = ilB
The net force on the wire = mg - F = mg - ilB
Downward acceleration of the wire due to current, \[a= \frac{mg - F}{m}\]
\[a = \frac{mg - ilB}{m}\]
\[a = g - \frac{B^2 l^2 v}{Rm} ..........\left[ \because i = \frac{Blv}{R} \right]\]
(d) Let the wire start moving with a constant velocity.
Now,
Let the speed of the wire be vm
As speed is constant, acceleration, a = 0
\[a = g - \frac{B^2 l^2 v_m}{Rm} = 0\]
\[\frac{B^2 l^2 v_m}{Rm} = g\]
\[ \Rightarrow v_m = \frac{gRm}{B^2 l^2}\]
(e) The acceleration of the wire can be expressed as time rate of change of velocity
\[\frac{dv}{dt} = a\]
\[\therefore \frac{dv}{dt} = \left( \frac{mg - B^2 l^2 v/R}{m} \right)\]
\[ \Rightarrow \frac{dv}{\frac{mg - B^2 l^2 v/R}{m}} = dt\]
\[ \int\limits_0^v \frac{m dv}{mg - \frac{B^2 l^2 v}{R}} = \int dt^t_0 \]
\[ \Rightarrow \frac{m}{- \frac{B^2 l^2}{R}} \left[ \log\left( mg - \frac{B^2 l^2 v}{R} \right) \right]_0^v = t\]
\[ \Rightarrow \frac{- mR}{B^2 l^2}\left[ \log\left( mg - \frac{B^2 l^2 v}{R} \right) - \log(mg) \right] = t\]
\[ \Rightarrow \log\left[ \frac{mg - \frac{B^2 l^2 v}{R}}{mg} \right] = \frac{- t B^2 l^2}{mR}\]
\[ \Rightarrow \log\left[ 1 - \frac{B^2 l^2 v}{Rmg} \right] = \frac{- t B^2 l^2}{mR}\]
\[ \Rightarrow 1 - \frac{B^2 l^2 v}{Rmg} = e^{- \frac{t B^2 l^2}{mR}} \]
\[ \Rightarrow \left( 1 - e^{- \frac{t B^2 l^2}{mR}} \right) = \frac{B^2 l^2 v}{Rmg}\]
\[v = \frac{Rmg}{B^2 l^2}\left( 1 - e^{- \frac{B^2 l^2 t}{mR}} \right)\]
\[ \Rightarrow v = v_m \left( 1 - e^{- \frac{gt}{v_m}} \right) ..........\left[ \because v_m = \frac{Rmg}{B^2 l^2} \right]\]
(f) The velocity can be expressed as time rate of change of position x is the position of the wire at instant t.
\[\because\frac{dx}{dt} = v\]
Thus, the displacement of the wire can be expressed as:-
\[s = \int_0^t dx = \int_0^t vdt\]
\[\therefore s = x_t - x_0 = v_m \int\limits_0^t \left( 1 - e^{- \frac{gt}{v_m}} \right) . dt\]
\[s = v_m . \left( t + \frac{v_m}{g} . e^{- \frac{gt}{v_m}} \right)_0^t \]
\[s = \left( v_m t + \frac{{v_m}^2}{g} e^{- \frac{gt}{v_m}} \right) - \frac{{v_m}^2}{g}\]
\[s = v_m t - \frac{{v_m}^2}{g}\left( 1 - e^{- \frac{gt}{v_m}} \right)\]
(g) Rate of development of heat in the wire is given by P = V × i
\[V = Blv\]
\[i = \frac{Blv}{R}\]
Therefore, the rate of development of heat in the wire is given by
\[P = Blv \times \frac{Blv}{R} = \frac{B^2 l^2 v^2}{R}\]
\[P = \frac{B^2 l^2 {v_m}^2 \left( 1 - e^{- \frac{gt}{v_m}} \right)^2}{R} ............\left[ \because v = v_m \left( 1 - e^{- \frac{gt}{v_m}} \right) \right]\]
Rate of decrease in potential energy is given by
\[\frac{dU}{dt} = \frac{d}{dt}(mgx) = mg . \frac{dx}{dt}\]
\[\frac{dU}{dt} = mgv\]
\[\frac{dU}{dt} = mg . v_m \left( 1 - e^{- \frac{gt}{v_m}} \right) .............\left[ \because v = v_m \left( 1 - e^{- \frac{gt}{v_m}} \right) \right]\]
After the steady state, i.e., t → ∞,
\[\frac{dU}{dt} = mg v_m \]
\[P = \frac{l^2 B^2}{R} {v_m}^2 \]
\[P = \frac{l^2 B^2}{R} \times v_m \times \frac{mgR}{l^2 B^2} ............\left[ \because v_m = \frac{mgR}{l^2 B^2} \right]\]
\[P = mg v_m\]
Thus, after the steady state,
\[P = \frac{dU}{dt}\]
APPEARS IN
संबंधित प्रश्न
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

Consider the situation shown in figure. The wire AB is slid on the fixed rails with a constant velocity. If the wire AB is replaced by a semicircular wire, the magnitude of the induced current will _____________ .

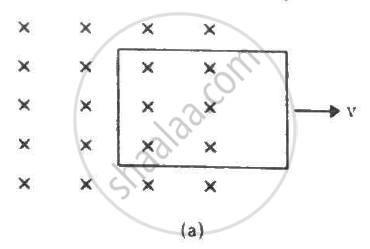
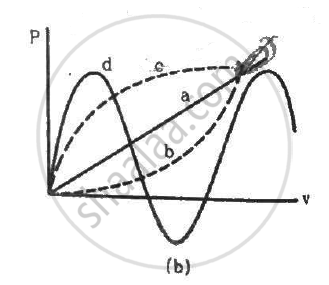
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
An LR circuit with a battery is connected at t = 0. Which of the following quantities is not zero just after the connection?
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
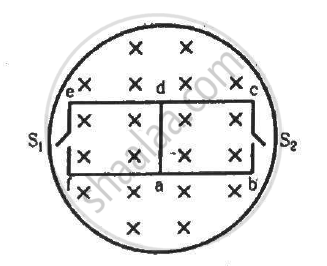
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
A closed coil having 100 turns is rotated in a uniform magnetic field B = 4.0 × 10−4 T about a diameter which is perpendicular to the field. The angular velocity of rotation is 300 revolutions per minute. The area of the coil is 25 cm2 and its resistance is 4.0 Ω. Find (a) the average emf developed in half a turn from a position where the coil is perpendicular to the magnetic field, (b) the average emf in a full turn and (c) the net charge displaced in part (a).
A 10 m wide spacecraft moves through the interstellar space at a speed 3 × 107 m s−1. A magnetic field B = 3 × 10−10 T exists in the space in a direction perpendicular to the plane of motion. Treating the spacecraft as a conductor, calculate the emf induced across its width.
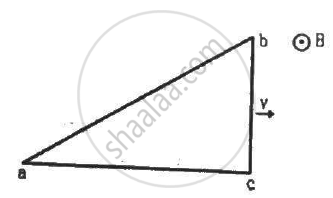
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
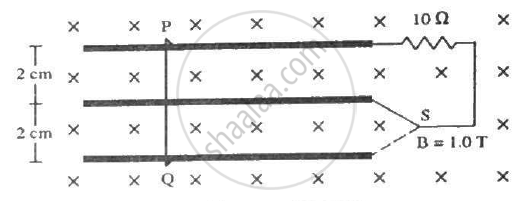
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s−1. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
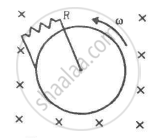
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
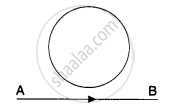
In the given figure current from A to B in the straight wire is decreasing. The direction of induced current in the loop is A ______.
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
