Advertisements
Advertisements
प्रश्न
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
उत्तर
Given,
Radius of the circular coil, R = 5.0 cm
Angular speed of circular coil, `omega=80` revolutions/minute
Magnetic field acting perpendicular to the axis of rotation, B = 0.010 T
The emf induced in the coil (e) is given by,
\[e = \frac{d\phi}{dt}\]
\[ \Rightarrow e = \frac{dB . A\cos\theta}{dt}\]
\[ \Rightarrow e = - BA\sin\theta\frac{d\theta}{dt}\]
`rArr e = −BAω sinθ ............((d theta)/(dt)=omega=" the rate of change of angle between the arc vector and B")`
(a) For maximum emf, sinθ = 1
∴ e = BAω
`rArr e=0.010xx25xx10^-4xx80xx(2pixxpi)/60`
⇒ e = 0.66 × 10−3 = 6.66 × 10−4 V
(b) The direction of the induced emf changes every instant. Thus, the average emf becomes zero.
(c) The emf induced in the coil is e = −BAωsinθ = −BAωsin ωt
The average of the squares of emf induced is given by
\[{e_{av}}^2 = \frac{\int_0^T B^2 A^2 \omega^2 \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \left( 1 - \cos2\omega t \right) dt}{2T}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T} \left[ t - \frac{\sin2\omega t}{2\omega} \right]_0^T \]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T}\left[ T - \frac{\sin4\pi - \sin 0}{2\omega} \right] = \frac{B^2 A^2 \omega^2}{2}\]
\[ \Rightarrow {e_{av}}^2 = \frac{(6 . 66 \times {10}^{- 4} )^2}{2} = 22 . 1778 \times {10}^{- 8} V^2...............\left[ \because BA\omega = 6 . 66 \times {10}^{- 4} V \right]\]
\[ \Rightarrow {e_{av}}^2 = 2 . 2 \times {10}^{- 7} V^2\]
APPEARS IN
संबंधित प्रश्न
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
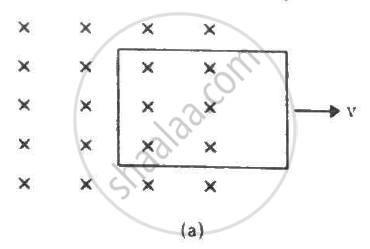
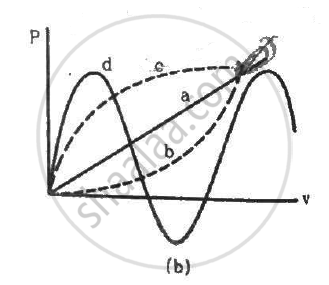
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
A conducting loop is placed in a uniform magnetic field with its plane perpendicular to the field. An emf is induced in the loop if ___________.
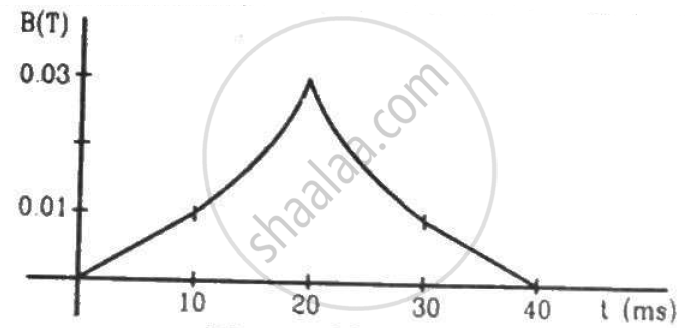
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
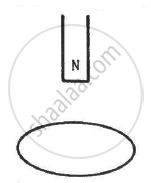
The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
A wire-loop confined in a plane is rotated in its own plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
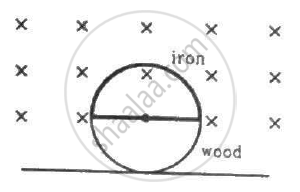
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
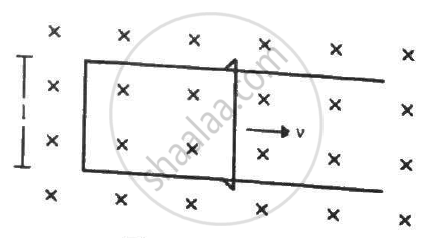
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
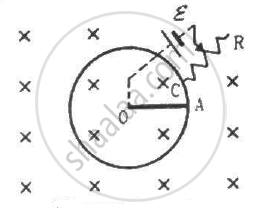
Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. A battery of emf ε and a variable resistance R are connected between O and C. Neglect the resistance of the connecting wires. Let θ be the angle made by the rod from the horizontal position (show in the figure), measured in the clockwise direction. During the part of the motion 0 < θ < π/4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magnetic field is reduced from its initial value of 0.3 T at the rate of 0.02 T s-1 If the cut is joined and loop has a resistance of 1.6 Ω, then how much power is dissipated by the loop as heat?
