Advertisements
Advertisements
प्रश्न
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
उत्तर
Given,
Radius of the circular coil, R = 5.0 cm
Angular speed of circular coil, `omega=80` revolutions/minute
Magnetic field acting perpendicular to the axis of rotation, B = 0.010 T
The emf induced in the coil (e) is given by,
\[e = \frac{d\phi}{dt}\]
\[ \Rightarrow e = \frac{dB . A\cos\theta}{dt}\]
\[ \Rightarrow e = - BA\sin\theta\frac{d\theta}{dt}\]
`rArr e = −BAω sinθ ............((d theta)/(dt)=omega=" the rate of change of angle between the arc vector and B")`
(a) For maximum emf, sinθ = 1
∴ e = BAω
`rArr e=0.010xx25xx10^-4xx80xx(2pixxpi)/60`
⇒ e = 0.66 × 10−3 = 6.66 × 10−4 V
(b) The direction of the induced emf changes every instant. Thus, the average emf becomes zero.
(c) The emf induced in the coil is e = −BAωsinθ = −BAωsin ωt
The average of the squares of emf induced is given by
\[{e_{av}}^2 = \frac{\int_0^T B^2 A^2 \omega^2 \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \left( 1 - \cos2\omega t \right) dt}{2T}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T} \left[ t - \frac{\sin2\omega t}{2\omega} \right]_0^T \]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T}\left[ T - \frac{\sin4\pi - \sin 0}{2\omega} \right] = \frac{B^2 A^2 \omega^2}{2}\]
\[ \Rightarrow {e_{av}}^2 = \frac{(6 . 66 \times {10}^{- 4} )^2}{2} = 22 . 1778 \times {10}^{- 8} V^2...............\left[ \because BA\omega = 6 . 66 \times {10}^{- 4} V \right]\]
\[ \Rightarrow {e_{av}}^2 = 2 . 2 \times {10}^{- 7} V^2\]
APPEARS IN
संबंधित प्रश्न
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

What is motional emf? State any two factors on which it depends.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
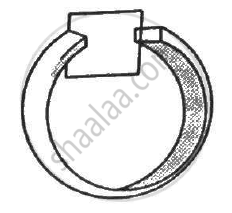
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
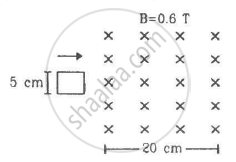
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
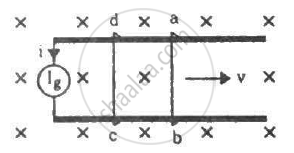
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.
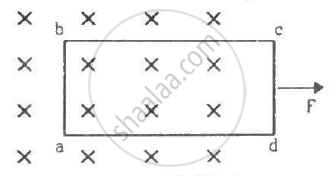
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
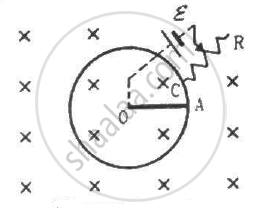
Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. A battery of emf ε and a variable resistance R are connected between O and C. Neglect the resistance of the connecting wires. Let θ be the angle made by the rod from the horizontal position (show in the figure), measured in the clockwise direction. During the part of the motion 0 < θ < π/4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
A small flat search coil of area 5cm2 with 140 closely wound turns is placed between the poles of a powerful magnet producing magnetic field 0.09T and then quickly removed out of the field region. Calculate:
(a) Change of magnetic flux through the coil, and
(b) emf induced in the coil.
A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
When the rate of change oic current is unity, the induced emf is equal to ______.
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magnetic field is reduced from its initial value of 0.3 T at the rate of 0.02 T s-1 If the cut is joined and loop has a resistance of 1.6 Ω, then how much power is dissipated by the loop as heat?
