Advertisements
Advertisements
प्रश्न
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
पर्याय
zero
`1/2Blomega^2`
Blω2
2Blω2
उत्तर
zero

Let us consider a small element dx at a distance x from the centre of the rod rotating with angular velocity ω about its perpendicular bisector. The emf induced in the small element of the rod because of its motion is given by
`de = Bomegaxdx`
The emf induced between the centre of the rod and one of its end is given by
\[\int de = \int_0^l B\omega xdx\]
\[ \Rightarrow e = B\omega \left[ \frac{x^2}{2} \right]_0^{l/2} \]
\[ \Rightarrow e = \frac{1}{8}B\omega l^2\]
The emf at both ends is the same. So, the potential difference between the two ends is zero.
APPEARS IN
संबंधित प्रश्न
A circular coil of radius 10 cm, 500 turns and resistance 200 Ω is placed with its plane perpendicular to the horizontal component of the Earth's magnetic field. It is rotated about its vertical diameter through 180° in 0.25 s. Estimate the magnitude of the emf and current induced in the coil. (Horizontal component of the Earth's magnetic field at the place is 3.0 ✕ 10−5 T).
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
Consider the following statements:-
(A) An emf can be induced by moving a conductor in a magnetic field.
(B) An emf can be induced by changing the magnetic field.
A conducting loop is placed in a uniform magnetic field with its plane perpendicular to the field. An emf is induced in the loop if ___________.
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
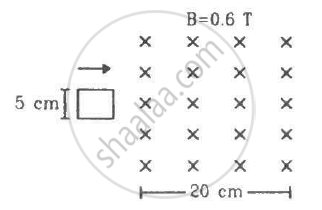
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
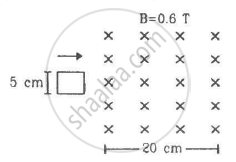
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.
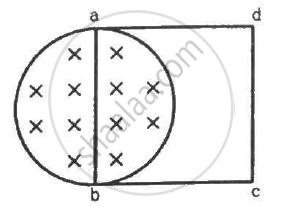
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
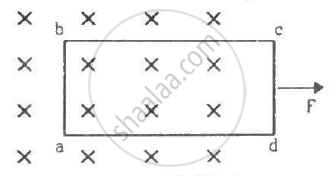
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
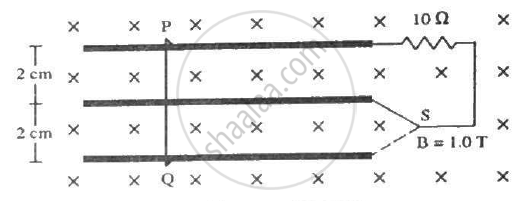
Consider the situation shown in figure. The wire PQ has a negligible resistance and is made to slide on the three rails with a constant speed of 5 cm s−1. Find the current in the 10 Ω resistor when the switch S is thrown to (a) the middle rail (b) the bottom rail.
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.
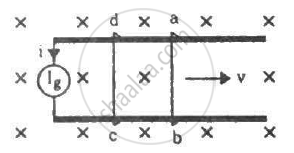
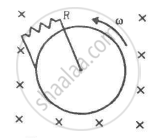
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
Plot a graph showing variation of induced e.m.f. with the rate of change of current flowing through a coil.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
