Advertisements
Advertisements
प्रश्न
A circular coil of radius 10 cm, 500 turns and resistance 200 Ω is placed with its plane perpendicular to the horizontal component of the Earth's magnetic field. It is rotated about its vertical diameter through 180° in 0.25 s. Estimate the magnitude of the emf and current induced in the coil. (Horizontal component of the Earth's magnetic field at the place is 3.0 ✕ 10−5 T).
उत्तर
Horizontal component of the Earth's magnetic field, B = 3 × 10−5 T
Radius of the coil, r = 10 cm = 0.1 m
Number of turns, N = 500
Resistance of the coil, R = 200 Ω
Angular speed of rotation of coil,
The Emf induced in the coil is a function of time and is given by
\[\omega = \frac{d\theta}{dt} = \frac{\pi}{0 . 25}\]
\[ \Rightarrow \omega = \frac{3 . 14}{0 . 25} = 12 . 56 \text { rad/s }\]
Area of the coil,
\[A = \pi r^2 \]
\[ \Rightarrow A = 3 . 14 \times (0 . 1 )^2 = 0 . 0314 m^2 \]
\[e = NAB\omega\sin\omega t\]
Maximum emf induced in the coil is given as,
\[e = NAB\omega\]
\[ \Rightarrow e = 500 \times 0 . 0314 \times 3 \times {10}^{- 5} \times 12 . 56\]
\[ \Rightarrow e = 5 . 91 \times {10}^{- 3} V\]
Maximum induced current in the coil is given as,
\[i = \frac{e}{R}\]
\[ \Rightarrow i = \frac{5 . 91 \times {10}^{- 3}}{200} = 2 . 95 \times {10}^{- 5} A\]
Disclaimer: As it is not mentioned in the question, that whether instantaneous or maximum value of the induced emf and current in the coil are to be calculated. Thus, the maximum values of induced emf and current are calculated. The instantaneous values of the induced emf and current are zero for the given instant.
APPEARS IN
संबंधित प्रश्न
Figure shows a metal rod PQ resting on the smooth rails AB and positioned between the poles of a permanent magnet. The rails, the rod, and the magnetic field are in three mutual perpendicular directions. A galvanometer G connects the rails through a switch K. Length of the rod = 15 cm, B = 0.50 T, resistance of the closed loop containing the rod = 9.0 mΩ. Assume the field to be uniform.
(a) Suppose K is open and the rod is moved with a speed of 12 cm s−1 in the direction shown. Give the polarity and magnitude of the induced emf.
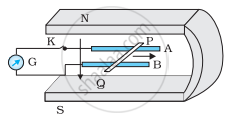
(b) Is there an excess charge built up at the ends of the rods when K is open? What if K is closed?
(c) With K open and the rod moving uniformly, there is no net force on the electrons in the rod PQ even though they do experience magnetic force due to the motion of the rod. Explain.
(d) What is the retarding force on the rod when K is closed?
(e) How much power is required (by an external agent) to keep the rod moving at the same speed = (12 cm s−1) when K is closed? How much power is required when K is open?
(f) How much power is dissipated as heat in the closed circuit? What is the source of this power?
(g) What is the induced emf in the moving rod if the magnetic field is parallel to the rails instead of being perpendicular?
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
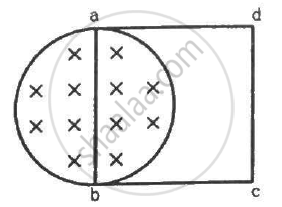
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
A 10 m wide spacecraft moves through the interstellar space at a speed 3 × 107 m s−1. A magnetic field B = 3 × 10−10 T exists in the space in a direction perpendicular to the plane of motion. Treating the spacecraft as a conductor, calculate the emf induced across its width.
The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h−1? The vertical component of earth's magnetic field is 0.2 × 10−4 T and the rails are separated by 1 m.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
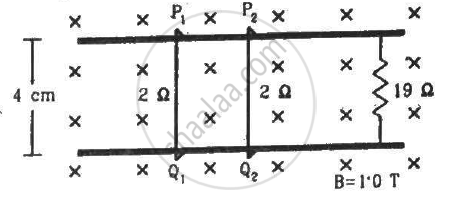
Consider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5 cm s−1. Find the electric current in the 19 Ω resistor if (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.
The current in an ideal, long solenoid is varied at a uniform rate of 0.01 As−1. The solenoid has 2000 turns/m and its radius is 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 2.0 seconds. (b) Find the electric field induced at a point on the circumference of the circle. (c) Find the electric field induced at a point outside the solenoid at a distance 8.0 cm from its axis.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
