Advertisements
Advertisements
प्रश्न
In the given circuit in the steady state, obtain the expressions for (a) the potential drop (b) the charge and (c) the energy stored in the capacitor, C.

उत्तर
(a)

In the steady state, the capacitor behaves as an open circuit. When the steady state is reached, there is no current through arm BE. The potential difference across the two plates of the capacitor is equal to the potential difference across EF.
Applying Kirchhoff's voltage law in the loop ACDF
\[- 2V + 2RI + RI + V = 0\]
\[V = 3RI\]
\[ \Rightarrow I = \frac{V}{3R}\]
\[V_E - V_B = 2V - \left( \frac{V}{3R} \right) \times 2R = \frac{4V}{3}\]
Since there is no current through the battery in branch BE, therefore,
\[V_E - V_B = \left( V_E - V_P \right) + \left( V_P - V_B \right)\]
\[\frac{4V}{3} = V_E - V_P + V\]
\[ \Rightarrow V_E - V_P = \frac{V}{3}\]
\[\left( b \right) \text { The charge stored in the capacitor }, Q = CV = \frac{CV}{3}\]
\[\left( c \right) \text { The energy stored in the capacitor, E } = \frac{1}{2}C \left( V_E - V_P \right)^2 = \frac{1}{2}C \left( \frac{V}{3} \right)^2 = \frac{1}{18}C V^2\]
APPEARS IN
संबंधित प्रश्न
Figure 3.34 shows a potentiometer circuit for comparison of two resistances. The balance point with a standard resistor R = 10.0 Ω is found to be 58.3 cm, while that with the unknown resistance X is 68.5 cm. Determine the value of X. What might you do if you failed to find a balance point with the given cell of emf ε?
In a potentiometer experiment, balancing length is found to be 120 cm for a cell E1 of emf 2V. What will be the balancing length for another cell E2 of emf 1.5V? (No other changes are made in the experiment.)
Draw a labelled circuit diagram of a potentiometer to compare emfs of two cells. Write the working formula (Derivation not required).
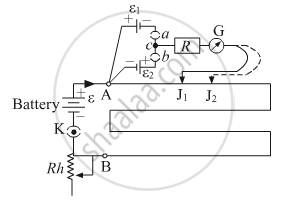
A student uses the circuit diagram of a potentiometer as shown in the figure
(a) for a steady current I passing through the potentiometer wire, he gets a null point for the cell ε1. and not for ε2. Give the reason for this observation and suggest how this difficulty can be resolved.
(b) What is the function of resistance R used in the circuit? How will the change in its value affect the null point?
(c) How can the sensitivity of the potentiometer be increased?
The resistance of a potentiometer wire is 8 Ω and its length is 8 m. A resistance box and a 2 V battery are connected in series with iL What should be the resistance in the box if it is desired to have a potential drop of 1 µV/mm?
Select the WRONG statement:
A potentiometer wire of length 'L' and a resistance 'r' are connected in series with a battery of E.M.F. 'E0' and a resistance 'r1'. A cell of unknown E.M.F, 'E' is balanced at a length 'ℓ' of the potentiometer wire. The unknown E.M.F. E is given by ______
In a potentiometer circuit, a cell of EMF 1.5 V gives balance point at 36 cm length of wire. If another cell of EMF 2.5 V replaces the first cell, then at what length of the wire, the balance point occurs?
What is the value of resistance for an ideal voltmeter?
Draw neat labelled diagram of potentiometer as voltage divider.
