Advertisements
Advertisements
Question
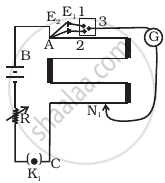
In the given circuit in the steady state, obtain the expressions for (a) the potential drop (b) the charge and (c) the energy stored in the capacitor, C.

Solution
(a)

In the steady state, the capacitor behaves as an open circuit. When the steady state is reached, there is no current through arm BE. The potential difference across the two plates of the capacitor is equal to the potential difference across EF.
Applying Kirchhoff's voltage law in the loop ACDF
\[- 2V + 2RI + RI + V = 0\]
\[V = 3RI\]
\[ \Rightarrow I = \frac{V}{3R}\]
\[V_E - V_B = 2V - \left( \frac{V}{3R} \right) \times 2R = \frac{4V}{3}\]
Since there is no current through the battery in branch BE, therefore,
\[V_E - V_B = \left( V_E - V_P \right) + \left( V_P - V_B \right)\]
\[\frac{4V}{3} = V_E - V_P + V\]
\[ \Rightarrow V_E - V_P = \frac{V}{3}\]
\[\left( b \right) \text { The charge stored in the capacitor }, Q = CV = \frac{CV}{3}\]
\[\left( c \right) \text { The energy stored in the capacitor, E } = \frac{1}{2}C \left( V_E - V_P \right)^2 = \frac{1}{2}C \left( \frac{V}{3} \right)^2 = \frac{1}{18}C V^2\]
APPEARS IN
RELATED QUESTIONS
Accuracy of potentiometer can be easily increased by ______.
State the principle of a potentiometer. Define potential gradient. Obtain an expression for potential gradient in terms of resistivity of the potentiometer wire.
Why is a potentiometer preferred over a voltmeter for measuring emf?
When the null point is obtained in the potentiometer, the current is drawn from the ______
The length of a potentiometer wire is L. A cell of e.m.f E is balanced at length L/3 from the positive end of the wire. If the length of wire increases by L/2, then the same cell will give balance point at length ____________.
In a potentiometer experiment, for measuring internal resistance of a cell, the balance point has been obtained on the fourth wire. The balance point can be shifted to fifth wire by ______.
In a potentiometer of 10 wires, the balance point is obtained on the 7th wire. To shift the balance point to 9th wire, we should ______.
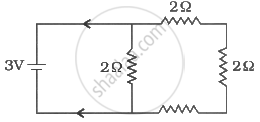
What is the current I in the circuit as show in fig.
Specific resistance of a conductor increase with.
In an experiment with a potentiometer, VB = 10V. R is adjusted to be 50Ω (Figure). A student wanting to measure voltage E1 of a battery (approx. 8V) finds no null point possible. He then diminishes R to 10Ω and is able to locate the null point on the last (4th) segment of the potentiometer. Find the resistance of the potentiometer wire and potential drop per unit length across the wire in the second case.