Advertisements
Advertisements
प्रश्न
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
उत्तर
Given:-
Self-inductance, L = 20 mH
Emf of the battery, e = 5.0 V
Resistance, R = 10 Ω
Now,
Time constant of the coil:-
\[\tau = \frac{L}{R} = \frac{20 \times {10}^{- 3}}{10}=2\times10^{-3} s\]
Steady-state current:-
\[i_0 = \frac{e}{R} = \frac{5}{10} = 0 . 5\]
The current in the LR circuit at time t is given by
i = i0(1 − e−t/τ)
⇒ i = i0 − i0e−t/τ
On differentiating both sides, we get
\[\frac{di}{dt} = \frac{i_0}{\tau} e^{- t/\tau}\]
The rate of change of the induced emf is given by
\[R\frac{di}{dt} = R\frac{i_0}{\tau} \times e^{- t/\tau}\]
(a) At time t = 0 s, the rate of change of the induced emf is given by
\[R\frac{di}{dt} = R\frac{i_0}{\tau}\]
\[ = 10 \times \frac{0 . 5}{2 \times {10}^{- 3}}\]
\[ = 2 . 5 \times {10}^3 V/s\]
(b) At time t = 10 ms, the rate of change of the induced emf is given by
\[R\frac{di}{dt} = R\frac{i_0}{\tau} \times e^{- t/\tau}\]
Now,
For t = 10 ms = 10 × 10−3 s = 10−2 s,
\[\frac{dE}{dt} = 10 \times \frac{5}{10} \times \frac{1}{2 \times {10}^{- 3}} \times e^{- 0 . 01/(2\times 10^{- 3})} \]
= 16.844 = 17 V/s
(c) At time t = 1 s, the rate of change of the induced emf is given by
\[\frac{dE}{dt} = \frac{Rdi}{dt} = R\frac{i_0}{\tau} \times e^{- t/\tau}\]
\[= 10 \times \frac{5 \times {10}^{- 1}}{2 \times {10}^{- 3}} \times e^{- 1/(2\times 10^{- 3})}\]
= 0.00 V/s
APPEARS IN
संबंधित प्रश्न
The current flowing through an inductor of self-inductance L is continuously increasing. Plot a graph showing the variation of
Induced emf versus dI/dt
What is motional emf? State any two factors on which it depends.
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
An LR circuit with a battery is connected at t = 0. Which of the following quantities is not zero just after the connection?
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
The north pole of a magnet is brought down along the axis of a horizontal circular coil (see the following figure). As a result, the flux through the coil changes from 0.35 weber to 0.85 weber in an interval of half a second. Find the average emf induced during this period. Is the induced current clockwise or anticlockwise as you look into the coil from the side of the magnet ?
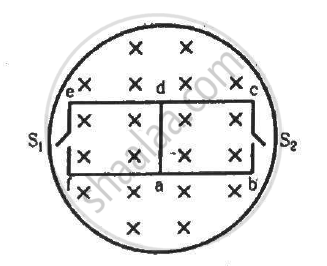
The magnetic field in the cylindrical region shown in figure increases at a constant rate of 20.0 mT/s. Each side of the square loop abcd and defa has a length of 1.00 cm and a resistance of 4.00 Ω. Find the current (magnitude and sense) in the wire ad if (a) the switch S1 is closed but S2 is open, (b) S1 is open but S2 is closed, (c) both S1 and S2 are open and (d) both S1 and S2 are closed.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
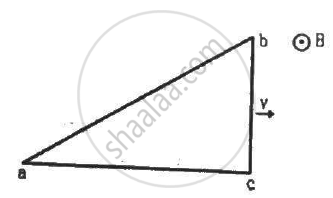
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
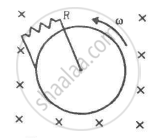
Figure shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i = i0 sin ωt. Find (a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to \[\frac{20\pi}{\omega}.\]
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
