Advertisements
Advertisements
Question
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
Solution
Given,
Radius of the circular coil, R = 5.0 cm
Angular speed of circular coil, `omega=80` revolutions/minute
Magnetic field acting perpendicular to the axis of rotation, B = 0.010 T
The emf induced in the coil (e) is given by,
\[e = \frac{d\phi}{dt}\]
\[ \Rightarrow e = \frac{dB . A\cos\theta}{dt}\]
\[ \Rightarrow e = - BA\sin\theta\frac{d\theta}{dt}\]
`rArr e = −BAω sinθ ............((d theta)/(dt)=omega=" the rate of change of angle between the arc vector and B")`
(a) For maximum emf, sinθ = 1
∴ e = BAω
`rArr e=0.010xx25xx10^-4xx80xx(2pixxpi)/60`
⇒ e = 0.66 × 10−3 = 6.66 × 10−4 V
(b) The direction of the induced emf changes every instant. Thus, the average emf becomes zero.
(c) The emf induced in the coil is e = −BAωsinθ = −BAωsin ωt
The average of the squares of emf induced is given by
\[{e_{av}}^2 = \frac{\int_0^T B^2 A^2 \omega^2 \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \sin^2 \omega t dt}{\int_0^T dt}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2 \int_0^T \left( 1 - \cos2\omega t \right) dt}{2T}\]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T} \left[ t - \frac{\sin2\omega t}{2\omega} \right]_0^T \]
\[ \Rightarrow {e_{av}}^2 = \frac{B^2 A^2 \omega^2}{2T}\left[ T - \frac{\sin4\pi - \sin 0}{2\omega} \right] = \frac{B^2 A^2 \omega^2}{2}\]
\[ \Rightarrow {e_{av}}^2 = \frac{(6 . 66 \times {10}^{- 4} )^2}{2} = 22 . 1778 \times {10}^{- 8} V^2...............\left[ \because BA\omega = 6 . 66 \times {10}^{- 4} V \right]\]
\[ \Rightarrow {e_{av}}^2 = 2 . 2 \times {10}^{- 7} V^2\]
APPEARS IN
RELATED QUESTIONS
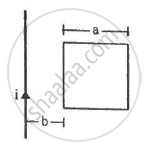
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth's magnetic field is 5 × 10–4 T and the angle of dip is 30°.
A metallic rod of length ‘l’ is rotated with a frequency v with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius r, about an axis passing through the centre and perpendicular to the plane of the ring. A constant uniform magnetic field B parallel to the axis is present everywhere. Using Lorentz force, explain how emf is induced between the centre and the metallic ring and hence obtained the expression for it.
Consider the situation shown in figure. The wire AB is slid on the fixed rails with a constant velocity. If the wire AB is replaced by a semicircular wire, the magnitude of the induced current will _____________ .

A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
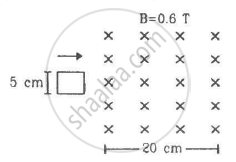
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
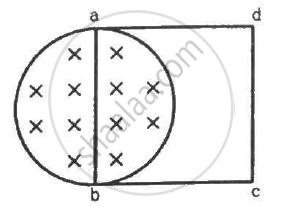
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
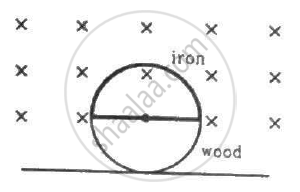
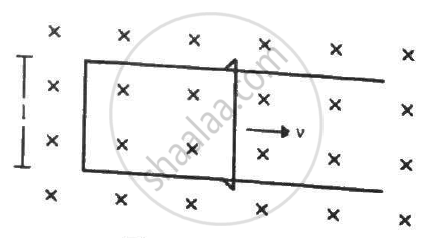
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
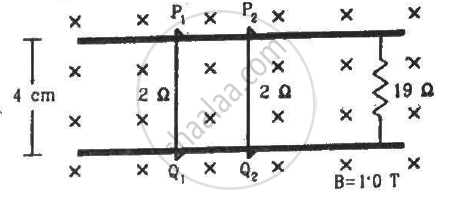
Consider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5 cm s−1. Find the electric current in the 19 Ω resistor if (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
Figure shows a square frame of wire having a total resistance r placed coplanarly with a long, straight wire. The wire carries a current i given by i = i0 sin ωt. Find (a) the flux of the magnetic field through the square frame, (b) the emf induced in the frame and (c) the heat developed in the frame in the time interval 0 to \[\frac{20\pi}{\omega}.\]
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
