Advertisements
Advertisements
Question
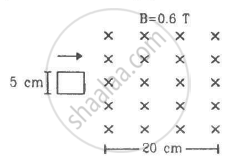
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the emf induced in the loop at (a) t = 2 s, (b) t = 10 s, (c) t = 22 s and (d) t = 30 s.
Solution
Given:-
Initial velocity, u = 1 cm/s
Magnetic field, B = 0.6 T
(a) At t = 2 s:-
Distance moved by the coil = 2 × 1 cm/s = 2 cm = 2 × 10-2m
Area under the magnetic field at t = 2s, A = 2 × 5 × 10-4m2
Initial magnetic flux = 0
Final magnetic flux = BA = 0.6 × (10 × 10-4)T-m2
Change in the magnetic flux, Δϕ = 0.6 × (10 × 10-4) - 0
Now, induced emf in the coil is
\[e = \frac{∆ \phi}{∆ t}\]
\[ = \frac{0 . 6 \times (10 - 0) \times {10}^{- 4}}{2}\]
\[ = 3 \times {10}^{- 4} V\]
(b) At t = 10 s:-
Distance moved by the coil = 10 × 1 = 10 cm
At this time square loop is completely inside the magnetic field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
(c) At t = 22 s:-
Distance moved = 22 × 1 = 22 cm
At this time loop is moving out of the field.
Initial magnetic flux = 0.6 × (5 × 5 × 10-4)T-m
At this time 2 cm part of the loop is ou t of the field.
Therefore, final magnetic flux = 0.6 × (3 × 5 × 10-4)T-m
Change in the magnetic flux, Δϕ = 0.6 × (3 × 5 × 10-4) - 0.6 × (5 × 5 × 10-4) = - 6 × 10-4)T-m2
Now, induced emf is
\[e = \frac{∆ \phi}{∆ t}\]
\[ = \frac{- 6 \times {10}^{- 4}}{2}\]
\[ = - 3 \times {10}^{- 4} V\]
(d) At t = 30 s:-
At this time loop is completely out of the field, so there is no change in the flux linked with the coil with time.
Therefore, induced emf in the coil at this time is zero.
APPEARS IN
RELATED QUESTIONS
An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth's magnetic field is 5 × 10–4 T and the angle of dip is 30°.
An LR circuit with a battery is connected at t = 0. Which of the following quantities is not zero just after the connection?
A conducting circular loop of area 1 mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from it. The straight wire carries an electric current which changes from 10 A to zero in 0.1 s. Find the average emf induced in the loop in 0.1 s.
A square-shaped copper coil has edges of length 50 cm and contains 50 turns. It is placed perpendicular to a 1.0 T magnetic field. It is removed from the magnetic field in 0.25 s and restored in its original place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
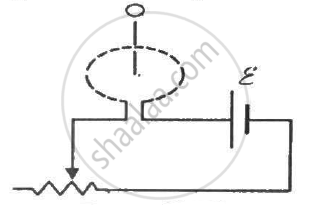
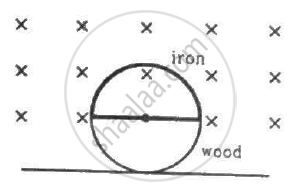
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
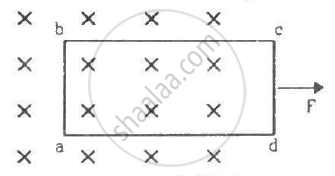
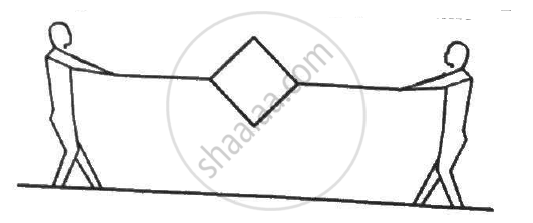
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
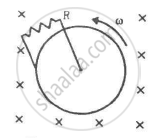
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

The current in an ideal, long solenoid is varied at a uniform rate of 0.01 As−1. The solenoid has 2000 turns/m and its radius is 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 2.0 seconds. (b) Find the electric field induced at a point on the circumference of the circle. (c) Find the electric field induced at a point outside the solenoid at a distance 8.0 cm from its axis.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
