Advertisements
Advertisements
Question
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
Solution
(i) Here, Ev = 110 V, R = 80 Ω, L = 0.1 H
θ = tan-1`(3/4)`
We know that in an L - R circuit
tan θ = `"Lω"/"R" = "X"_"L"/"R"`
`3/4 = "X"_"L"/80`
`"X"_"L" = 80 x 3/4` = 60 Ω
(ii) impedance Z = `sqrt( "X"_L^2 + "R"^2 )`
Z = `sqrt( (60)^2 + (80)^2 )`
Z = 100 Ω
(ii) Now,
`"I"_"v" = "E"_"v"/"Z" = 110/100 = 1.1 "A"`
(iv) XL = 2πnL
∴ n = `"X"_"L"/(2π"L") = 60/( 2 xx 3.14 xx 0.1 ) = 95.54 "Hz"`.
APPEARS IN
RELATED QUESTIONS
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is ______________ .
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
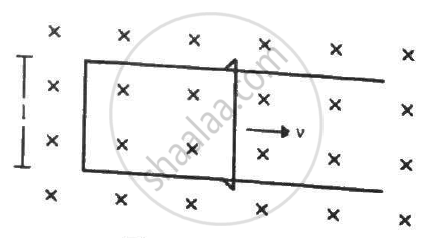
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
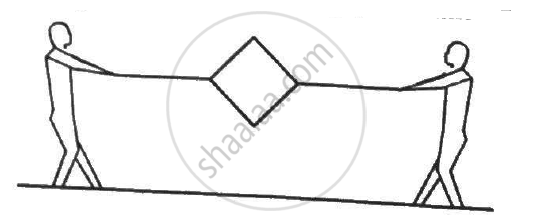
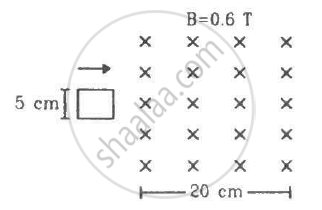
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
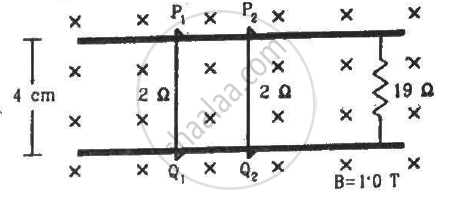
Consider the situation shown in figure. The wires P1Q1 and P2Q2 are made to slide on the rails with the same speed 5 cm s−1. Find the electric current in the 19 Ω resistor if (a) both the wires move towards right and (b) if P1Q1 moves towards left but P2Q2 moves towards right.
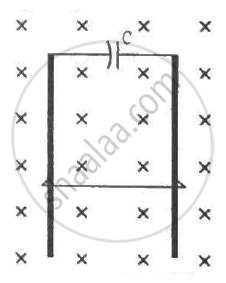
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.