Advertisements
Advertisements
Question
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
Solution
Given:-
Number of turns of the coil, N = 50
Magnetic field through the circular coil,
\[\overrightarrow B=0.200 \text{ T}\]
Radius of the circular coil, r = 2.00 cm = 0.02 m
Angle through which the coil is rotated, θ = 60°
Time taken to rotate the coil, t = 0.100 s
(a) The emf induced in the coil is given by
\[e = - \frac{N ∆ \phi}{∆ t} = \frac{N( \overrightarrow{B_f} . \overrightarrow{A}_f - \overrightarrow{B_i} . \overrightarrow{A}_i )}{T}\]
\[ = \frac{NB . A (\cos 0^\circ - \cos 60^\circ)}{T}\]
\[ = \frac{50 \times 2 \times {10}^{- 1} \times \pi(0 . 02 )^2}{2 \times 0 . 1}\]
\[ = 5 \times 4 \times {10}^{- 5} \times \pi\]
\[ = 2\pi \times {10}^{- 2} V = 6 . 28 \times {10}^{- 3} V\]
(b) The current in the coil is given by
\[i = \frac{e}{R} = \frac{6 . 28 \times {10}^{- 3}}{4}\]
\[ = 1 . 57 \times {10}^{- 3} A\]
The net charge passing through the cross section of the wire is given by
\[Q = it = 1 . 57 \times {10}^{- 3} \times {10}^{- 1} \]
\[ = 1 . 57 \times {10}^{- 4} C\]
APPEARS IN
RELATED QUESTIONS
The current flowing through an inductor of self-inductance L is continuously increasing. Plot a graph showing the variation of
Induced emf versus dI/dt
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

A circular coil of radius 10 cm, 500 turns and resistance 200 Ω is placed with its plane perpendicular to the horizontal component of the Earth's magnetic field. It is rotated about its vertical diameter through 180° in 0.25 s. Estimate the magnitude of the emf and current induced in the coil. (Horizontal component of the Earth's magnetic field at the place is 3.0 ✕ 10−5 T).
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is ______________ .
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
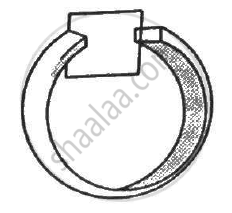
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
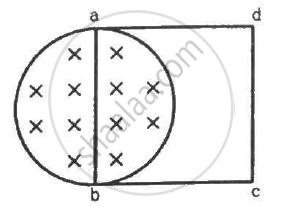
A wire of length 10 cm translates in a direction making an angle of 60° with its length. The plane of motion is perpendicular to a uniform magnetic field of 1.0 T that exists in the space. Find the emf induced between the ends of the rod if the speed of translation is 20 cm s−1.
A bicycle is resting on its stand in the east-west direction and the rear wheel is rotated at an angular speed of 100 revolutions per minute. If the length of each spoke is 30.0 cm and the horizontal component of the earth's magnetic field is 2.0 × 10−5 T, find the emf induced between the axis and the outer end of a spoke. Neglect centripetal force acting on the free electrons of the spoke.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
A small flat search coil of area 5cm2 with 140 closely wound turns is placed between the poles of a powerful magnet producing magnetic field 0.09T and then quickly removed out of the field region. Calculate:
(a) Change of magnetic flux through the coil, and
(b) emf induced in the coil.
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
When the rate of change oic current is unity, the induced emf is equal to ______.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
A rectangular loop of sides 8 cm and 2 cm with a small cut is stationary in a uniform magnetic field directed normal to the loop. The magnetic field is reduced from its initial value of 0.3 T at the rate of 0.02 T s-1 If the cut is joined and loop has a resistance of 1.6 Ω, then how much power is dissipated by the loop as heat?
