Advertisements
Advertisements
प्रश्न
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
उत्तर
Given:-
Number of turns of the coil, N = 50
Magnetic field through the circular coil,
\[\overrightarrow B=0.200 \text{ T}\]
Radius of the circular coil, r = 2.00 cm = 0.02 m
Angle through which the coil is rotated, θ = 60°
Time taken to rotate the coil, t = 0.100 s
(a) The emf induced in the coil is given by
\[e = - \frac{N ∆ \phi}{∆ t} = \frac{N( \overrightarrow{B_f} . \overrightarrow{A}_f - \overrightarrow{B_i} . \overrightarrow{A}_i )}{T}\]
\[ = \frac{NB . A (\cos 0^\circ - \cos 60^\circ)}{T}\]
\[ = \frac{50 \times 2 \times {10}^{- 1} \times \pi(0 . 02 )^2}{2 \times 0 . 1}\]
\[ = 5 \times 4 \times {10}^{- 5} \times \pi\]
\[ = 2\pi \times {10}^{- 2} V = 6 . 28 \times {10}^{- 3} V\]
(b) The current in the coil is given by
\[i = \frac{e}{R} = \frac{6 . 28 \times {10}^{- 3}}{4}\]
\[ = 1 . 57 \times {10}^{- 3} A\]
The net charge passing through the cross section of the wire is given by
\[Q = it = 1 . 57 \times {10}^{- 3} \times {10}^{- 1} \]
\[ = 1 . 57 \times {10}^{- 4} C\]
APPEARS IN
संबंधित प्रश्न
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

A rod of length l rotates with a small but uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the centre of the rod and an end is ______________ .
Consider the following statements:-
(A) An emf can be induced by moving a conductor in a magnetic field.
(B) An emf can be induced by changing the magnetic field.
An LR circuit with a battery is connected at t = 0. Which of the following quantities is not zero just after the connection?
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
A conducting loop of face-area A and resistance R is placed perpendicular to a magnetic field B. The loop is withdrawn completely from the field. Find the charge which flows through any cross-section of the wire in the process. Note that it is independent of the shape of the loop as well as the way it is withdrawn.
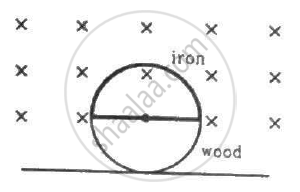
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
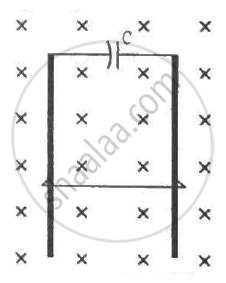
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

Two identical coaxial coils P and Q carrying equal amount of current in the same direction are brought nearer. The current in ______.
In the given figure current from A to B in the straight wire is decreasing. The direction of induced current in the loop is A ______.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
