Advertisements
Advertisements
Question
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
Solution
(a) Here, the magnetic field \[\overrightarrow B\] due to the long wire varies along the length of the rod.
We will consider a small element of the rod of length da at a distance a from the wire. The magnetic field at a distance a is given by
\[\overrightarrow{B} = \frac{\mu_0 i}{2\pi a}\]
Now,
Induced emf in the rod:-
\[de = Bvda\]
\[de = \frac{\mu_0 i}{2\pi a} \times v \times da\]
Integrating `x-l/2` and `x+l/2,` we get
\[e = \int\limits_{x - \frac{l}{2}}^{x + \frac{l}{2}} de\]
\[ = \int\limits_{x - \frac{l}{2}}^{x + \frac{l}{2}}\frac{\mu_0 i}{2\pi a} vda\]
\[ = \frac{\mu_0 iv}{2\pi}\left[ \ln\left( x + \frac{l}{2} \right) - \ln\left( x - \frac{l}{2} \right) \right]\]
\[ = \frac{\mu_0 iv}{2\pi}\ln\left[ \frac{x + \frac{l}{2}}{x - \frac{l}{2}} \right]\]
Emf induced in the rod due to the current-carrying wire:-
\[e = \frac{\mu_0 iv}{2\pi}\ln\left( \frac{2x + l}{2x - l} \right)\]
Now, let the current produced in the circuit containing the rod and the resistance be i'.
\[i' = \frac{e}{R}\]
\[ = \frac{\mu_0 iv}{2\pi R}\ln\left( \frac{2x + 1}{2x - 1} \right)\]
Force on the element:-
dF = i'Bl
\[\Rightarrow dF = \frac{\mu_0 iv}{2\pi R}\ln\left( \frac{2x + l}{2x - l} \right) \times \left( \frac{\mu_0 i}{2\pi a} \right) \times da\]
\[ = \left( \frac{\mu_0 i}{2\pi} \right)^2 \frac{v}{R}\ln\left( \frac{2x + l}{2x - l} \right)\frac{dx}{a}\]
And,
\[F = \left( \frac{\mu_0 i}{2\pi} \right)^2 \frac{v}{R}\ln\left( \frac{2x + l}{2x - l} \right) \int\limits_{x - \frac{l}{2}}^{x + \frac{l}{2}} \frac{da}{a}\]
\[ = \left( \frac{\mu_0 i}{2\pi} \right)^2 \frac{v}{R}\ln\left( \frac{2x + l}{2x - l} \right)\ln\left( \frac{2x + l}{2x - l} \right)\]
\[ = \frac{v}{R} \left[ \frac{\mu_0 i}{2\pi}\ln\left( \frac{2x + l}{2x - l} \right) \right]^2\]
(b) Current, \[i' = \frac{e}{R} = \frac{\mu_0 iv}{2\pi R}\ln\left( \frac{2x + l}{2x - l} \right)\]
(c) The rate of heat, that is, power, developed is given by
w = i2 R
\[w = \left[ \frac{\mu_0 iv}{2\pi R}\ln\left( \frac{2x + l}{2x - l} \right) \right]^2 R\]
\[ = \frac{1}{R} \left[ \frac{\mu_0 iv}{2\pi}\ln\left( \frac{2x + l}{2x - l} \right) \right]^2\]
(d) Power delivered by the external agency is the same as the rate of heat developed.
Here,
p = i2R
\[= \frac{1}{R} \left[ \frac{\mu_0 iv}{2\pi}\ln\left( \frac{2x + l}{2x - l} \right) \right]^2\]
APPEARS IN
RELATED QUESTIONS
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
What is motional emf? State any two factors on which it depends.
Two circular loops are placed coaxially but separated by a distance. A battery is suddenly connected to one of the loops establishing a current in it. Will there be a current induced in the other loop? If yes, when does the current start and when does it end? Do the loops attract each other or do they repel?
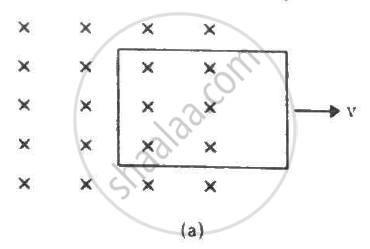
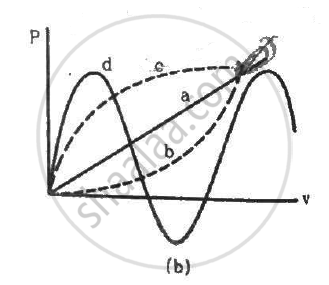
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is __________________ .
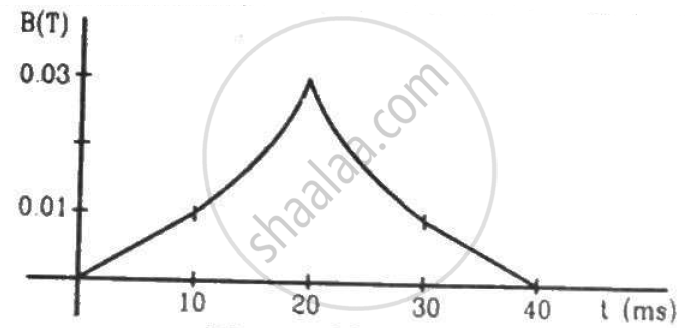
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
A wire-loop confined in a plane is rotated in its own plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
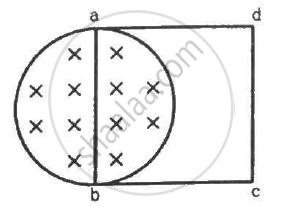
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
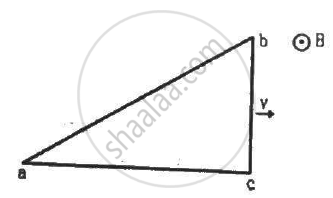
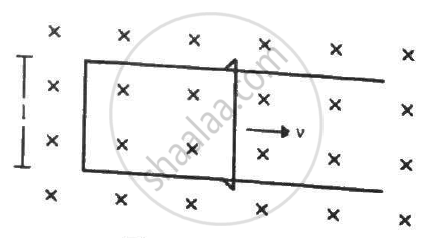
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
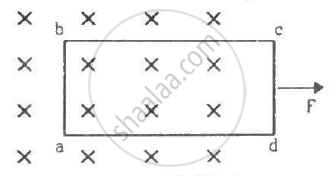
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
The current in an ideal, long solenoid is varied at a uniform rate of 0.01 As−1. The solenoid has 2000 turns/m and its radius is 6.0 cm. (a) Consider a circle of radius 1.0 cm inside the solenoid with its axis coinciding with the axis of the solenoid. Write the change in the magnetic flux through this circle in 2.0 seconds. (b) Find the electric field induced at a point on the circumference of the circle. (c) Find the electric field induced at a point outside the solenoid at a distance 8.0 cm from its axis.
The current in a solenoid of 240 turns, having a length of 12 cm and a radius of 2 cm, changes at a rate of 0.8 A s−1. Find the emf induced in it.
Two identical coaxial coils P and Q carrying equal amount of current in the same direction are brought nearer. The current in ______.
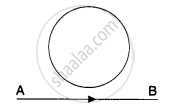
In the given figure current from A to B in the straight wire is decreasing. The direction of induced current in the loop is A ______.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
