Advertisements
Advertisements
Question
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.
Solution
(a) The emf induced between the ends of the wire is calculated using the following formula:-
e = Bv (Effective length of the wire)
Effective length of the wire = Component of length perpendicular to the velocity
Here, the component of length moving perpendicular to v is 2r.
∴ Induced emf, e = Bv2r
(b) When the velocity is parallel to the diameter of the semicircular wire, the component of its length perpendicular to its velocity is zero.
∴ Induced emf, e = 0
APPEARS IN
RELATED QUESTIONS
State Lenz’s Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
Consider the situation shown in figure. The wire AB is slid on the fixed rails with a constant velocity. If the wire AB is replaced by a semicircular wire, the magnitude of the induced current will _____________ .

A conducting loop of area 5.0 cm2 is placed in a magnetic field which varies sinusoidally with time as B = B0 sin ωt where B0 = 0.20 T and ω = 300 s−1. The normal to the coil makes an angle of 60° with the field. Find (a) the maximum emf induced in the coil, (b) the emf induced at τ = (π/900)s and (c) the emf induced at t = (π/600) s.
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
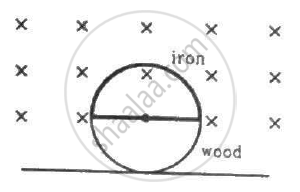
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
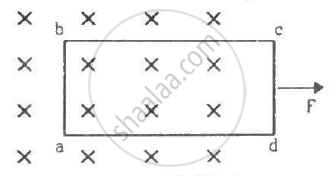
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
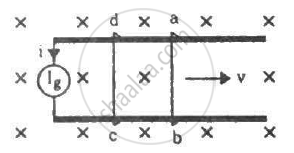
The current generator Ig' shown in figure, sends a constant current i through the circuit. The wire cd is fixed and ab is made to slide on the smooth, thick rails with a constant velocity v towards right. Each of these wires has resistance r. Find the current through the wire cd.
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) What would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a function of time. (g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
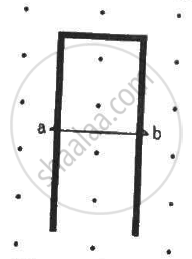
Figure shows a conducting disc rotating about its axis in a perpendicular magnetic field B. A resistor of resistance R is connected between the centre and the rim. Calculate the current in the resistor. Does it enter the disc or leave it at the centre? The radius of the disc is 5.0 cm, angular speed ω = 10 rad/s, B = 0.40 T and R = 10 Ω.
The magnetic field in a region is given by \[\overrightarrow{B} = \overrightarrow{k} \frac{B_0}{L}y\] where L is a fixed length. A conducting rod of length L lies along the Y-axis between the origin and the point (0, L, 0). If the rod moves with a velocity v = v0 \[\overrightarrow{i},\] find the emf induced between the ends of the rod.
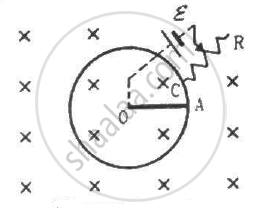
Suppose the circular loop lies in a vertical plane. The rod has a mass m. The rod and the loop have negligible resistances but the wire connecting O and C has a resistance R. The rod is made to rotate with a uniform angular velocity ω in the clockwise direction by applying a force at the midpoint of OA in a direction perpendicular to it. A battery of emf ε and a variable resistance R are connected between O and C. Neglect the resistance of the connecting wires. Let θ be the angle made by the rod from the horizontal position (show in the figure), measured in the clockwise direction. During the part of the motion 0 < θ < π/4 the only forces acting on the rod are gravity and the forces exerted by the magnetic field and the pivot. However, during the part of the motion, the resistance R is varied in such a way that the rod continues to rotate with a constant angular velocity ω. Find the value of R in terms of the given quantities.
An inductor-coil of inductance 20 mH having resistance 10 Ω is joined to an ideal battery of emf 5.0 V. Find the rate of change of the induced emf at (a) t = 0, (b) t = 10 ms and (c) t = 1.0 s.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
A conducting square loop of side 'L' and resistance 'R' moves in its plane with the uniform velocity 'v' perpendicular to one of its sides. A magnetic induction 'B' constant in time and space pointing perpendicular and into the plane of the loop exists everywhere as shown in the figure. The current induced in the loop is ______.
