Advertisements
Advertisements
प्रश्न
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
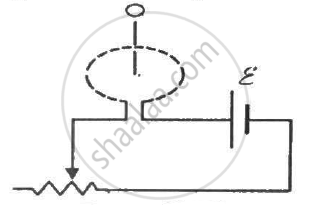
उत्तर
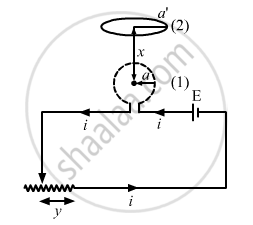
The magnetic field due to coil 1 at the centre of coil 2 is given by
\[B = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\]
The flux linked with coil 2 is given by
\[\phi = B . A' = \frac{\mu_0 Ni a^2}{2 ( a^2 + x^2 )^{3/2}}\pi a '^2\]
Now, let y be the distance of the sliding contact from its left end.
Given:-
\[v = \frac{dy}{dt}\]
Total resistance of the rheostat = R
When the distance of the sliding contact from the left end is y, the resistance of the rheostat (R') is given by
\[R' = \frac{R}{L}y\]
The current in the coil is the function of distance y travelled by the sliding contact of the rheostat. It is given by
\[i = \frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
The magnitude of the emf induced can be calculated as:-
\[e = \frac{d\phi}{dt} = \frac{\mu_0 N a^2 a '^2 \pi}{2 ( a^2 + x^2 )^{3/2}}\frac{di}{dt}\]
\[\Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\frac{d}{dt}\frac{\epsilon}{\left( \frac{R}{L}y + r \right)}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2 ( a^2 + x^2 )^{3/2}}\left[ \epsilon\frac{\left( - \frac{R}{L}v \right)}{\left( \frac{R}{L}y + r \right)^2} \right]\]
(a) For y = L,
\[e = \frac{\mu_0 N \pi a^2 a '^2 \epsilon Rv}{2L ( a^2 + x^2 )^{3/2} (R + r )^2}\]
(b) For y = L/2,
\[\frac{R}{L}y = \frac{R}{2}\]
\[ \Rightarrow e = \frac{\mu_0 N \pi a^2 a '^2}{2L( a^2 + x^2 )^{3/2}}\frac{\epsilon Rv}{\left( \frac{R}{2} + r \right)^2}\]
APPEARS IN
संबंधित प्रश्न
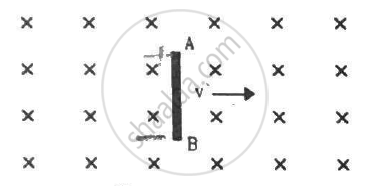
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
The flux of magnetic field through a closed conducting loop changes with time according to the equation, Φ = at2 + bt + c. (a) Write the SI units of a, b and c. (b) If the magnitudes of a, b and c are 0.20, 0.40 and 0.60 respectively, find the induced emf at t = 2 s.
A conducting circular loop of area 1 mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from it. The straight wire carries an electric current which changes from 10 A to zero in 0.1 s. Find the average emf induced in the loop in 0.1 s.
A wire-loop confined in a plane is rotated in its own plane with some angular velocity. A uniform magnetic field exists in the region. Find the emf induced in the loop.
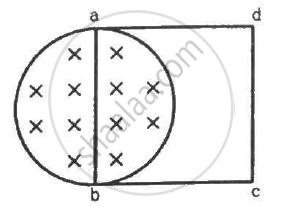
A uniform magnetic field B exists in a cylindrical region of radius 10 cm as shown in figure. A uniform wire of length 80 cm and resistance 4.0 Ω is bent into a square frame and is placed with one side along a diameter of the cylindrical region. If the magnetic field increases at a constant rate of 0.010 T/s, find the current induced in the frame.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
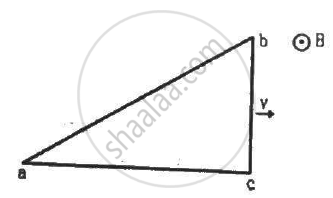
A right-angled triangle abc, made from a metallic wire, moves at a uniform speed v in its plane as shown in figure. A uniform magnetic field B exists in the perpendicular direction. Find the emf induced (a) in the loop abc, (b) in the segment bc, (c) in the segment ac and (d) in the segment ab.
A circular copper-ring of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the ring. Consider different pairs of diametrically opposite points on the ring. (a) Between which pair of points is the emf maximum? What is the value of this maximum emf? (b) Between which pair of points is the emf minimum? What is the value of this minimum emf ?
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
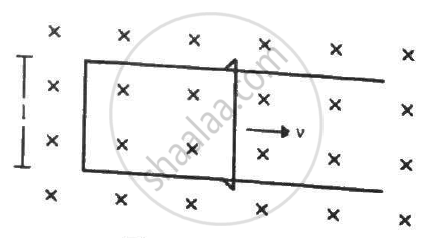
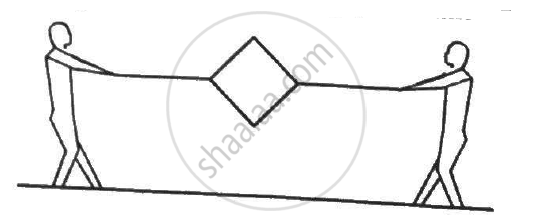
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
A rod of length l rotates with a uniform angular velocity ω about its perpendicular bisector. A uniform magnetic field B exists parallel to the axis of rotation. The potential difference between the two ends of the rod is ___________ .
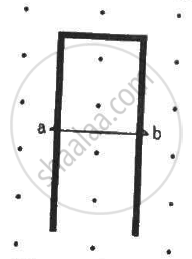
A conducting wire ab of length l, resistance r and mass m starts sliding at t = 0 down a smooth, vertical, thick pair of connected rails as shown in figure. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the rails. (a) Write the induced emf in the loop at an instant t when the speed of the wire is v. (b) What would be the magnitude and direction of the induced current in the wire? (c) Find the downward acceleration of the wire at this instant. (d) After sufficient time, the wire starts moving with a constant velocity. Find this velocity vm. (e) Find the velocity of the wire as a function of time. (f) Find the displacement of the wire as a function of time. (g) Show that the rate of heat developed in the wire is equal to the rate at which the gravitational potential energy is decreased after steady state is reached.
Consider a situation similar to that of the previous problem except that the ends of the rod slide on a pair of thick metallic rails laid parallel to the wire. At one end the rails are connected by resistor of resistance R. (a) What force is needed to keep the rod sliding at a constant speed v? (b) In this situation what is the current in the resistance R? (c) Find the rate of heat developed in the resistor. (d) Find the power delivered by the external agent exerting the force on the rod.
The mutual inductance between two coils is 2.5 H. If the current in one coil is changed at the rate of 1 As−1, what will be the emf induced in the other coil?
A small flat search coil of area 5cm2 with 140 closely wound turns is placed between the poles of a powerful magnet producing magnetic field 0.09T and then quickly removed out of the field region. Calculate:
(a) Change of magnetic flux through the coil, and
(b) emf induced in the coil.
An induced e.m.f. is produced when a magnet is plunged into a coil. The strength of the induced e.m.f. is independent of ______.
The current flowing in a step-down transformer 220 V to 22 V having impedance 220 π is
