Advertisements
Advertisements
प्रश्न
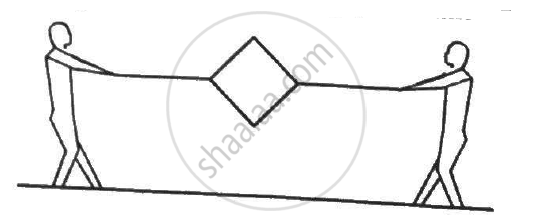
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
उत्तर
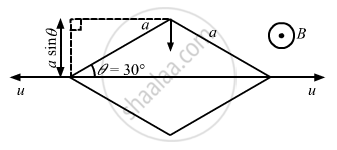
(a) The effective length of each side is the length that is perpendicular to the velocity of the corners.
Thus, the effective length of each side is a sin θ.
Net effective length for four sides = 4 × `a/2` = 2a
∴ Induced emf = Bvl = 2Bau
(b) Current in the frame is given by
\[i= \frac{e}{R} = \frac{2auB}{R}\]
(c) Total charge q, which flows through the sides of the frame, is given by
\[q = \frac{∆ \phi}{R}\]
Here,
ΔΦ = Change in the flux
R = Resistance of the coil
\[\therefore q = \frac{∆ \phi}{R}\]
\[= \frac{B( a^2 - 0)}{R}\]
\[ = \frac{B a^2}{R}\]
APPEARS IN
संबंधित प्रश्न
Two cells of emf E1 and E2 and internal resistances r1 and r2 are connected in parallel. Derive the expression for the (i) emf and (ii) internal resistance of a single equivalent cell which can replace this combination.
A square loop of side 12 cm with its sides parallel to X and Y axes is moved with a velocity of 8 cm s−1 in the positive x-direction in an environment containing a magnetic field in the positive z-direction. The field is neither uniform in space nor constant in time. It has a gradient of 10−3 T cm−1 along the negative x-direction (that is it increases by 10− 3 T cm−1 as one move in the negative x-direction), and it is decreasing in time at the rate of 10−3 T s−1. Determine the direction and magnitude of the induced current in the loop if its resistance is 4.50 mΩ.
A circular coil of radius 10 cm, 500 turns and resistance 200 Ω is placed with its plane perpendicular to the horizontal component of the Earth's magnetic field. It is rotated about its vertical diameter through 180° in 0.25 s. Estimate the magnitude of the emf and current induced in the coil. (Horizontal component of the Earth's magnetic field at the place is 3.0 ✕ 10−5 T).
State Lenz’s Law.
A metallic rod held horizontally along east-west direction, is allowed to fall under gravity. Will there be an emf induced at its ends? Justify your answer.
A small, conducting circular loop is placed inside a long solenoid carrying a current. The plane of the loop contains the axis of the solenoid. If the current in the solenoid is varied, the current induced in the loop is __________________ .
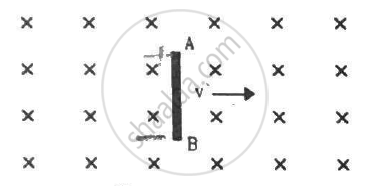
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
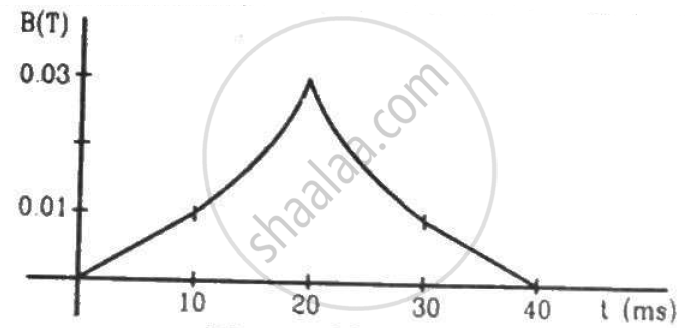
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
A conducting circular loop of area 1 mm2 is placed coplanarly with a long, straight wire at a distance of 20 cm from it. The straight wire carries an electric current which changes from 10 A to zero in 0.1 s. Find the average emf induced in the loop in 0.1 s.
Suppose the resistance of the coil in the previous problem is 25Ω. Assume that the coil moves with uniform velocity during its removal and restoration. Find the thermal energy developed in the coil during (a) its removal, (b) its restoration and (c) its motion.
A circular coil of one turn of radius 5.0 cm is rotated about a diameter with a constant angular speed of 80 revolutions per minute. A uniform magnetic field B = 0.010 T exists in a direction perpendicular to the axis of rotation. Find (a) the maximum emf induced, (b) the average emf induced in the coil over a long period and (c) the average of the squares of emf induced over a long period.
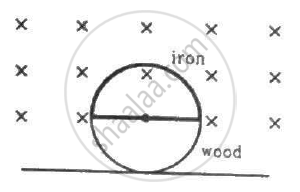
Figure shows a circular wheel of radius 10.0 cm whose upper half, shown dark in the figure, is made of iron and the lower half of wood. The two junctions are joined by an iron rod. A uniform magnetic field B of magnitude 2.00 × 10−4 T exists in the space above the central line as suggested by the figure. The wheel is set into pure rolling on the horizontal surface. If it takes 2.00 seconds for the iron part to come down and the wooden part to go up, find the average emf induced during this period.
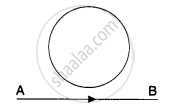
A copper wire bent in the shape of a semicircle of radius r translates in its plane with a constant velocity v. A uniform magnetic field B exists in the direction perpendicular to the plane of the wire. Find the emf induced between the ends of the wire if (a) the velocity is perpendicular to the diameter joining free ends, (b) the velocity is parallel to this diameter.
The magnetic field in a region is given by \[\overrightarrow{B} = \overrightarrow{k} \frac{B_0}{L}y\] where L is a fixed length. A conducting rod of length L lies along the Y-axis between the origin and the point (0, L, 0). If the rod moves with a velocity v = v0 \[\overrightarrow{i},\] find the emf induced between the ends of the rod.
A uniform magnetic field B exists in a cylindrical region, shown dotted in figure. The magnetic field increases at a constant rate `(dB)/(dt).` Consider a circle of radius r coaxial with the cylindrical region. (a) Find the magnitude of the electric field E at a point on the circumference of the circle. (b) Consider a point P on the side of the square circumscribing the circle. Show that the component of the induced electric field at P along ba is the same as the magnitude found in part (a).

The magnetic potential energy stored in a certain inductor is 25 mJ, when the current in the inductor is 60 mA. This inductor is of inductance ______.
A current carrying infinitely long wire is kept along the diameter of a circular wire loop, without touching it, the correct statement(s) is(are)
- The emf induced in the loop is zero if the current is constant.
- The emf induced in the loop is finite if the current is constant.
- The emf induced in the loop is zero if the current decreases at a steady rate.
In the given figure current from A to B in the straight wire is decreasing. The direction of induced current in the loop is A ______.
A sinusoidal voltage V(t) = 100 sin (500 t) is applied across a pure inductance of L = 0.02 H. The current through the coil is:
