Advertisements
Advertisements
प्रश्न
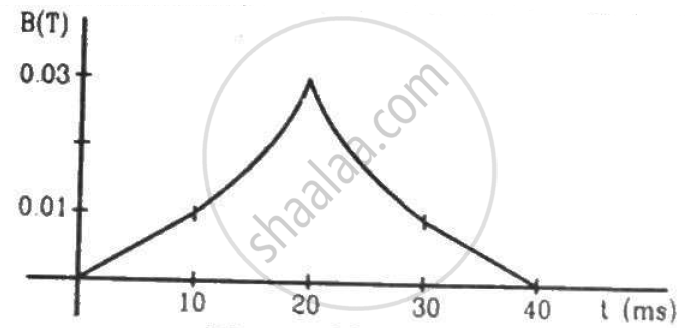
(a) The magnetic field in a region varies as shown in figure. Calculate the average induced emf in a conducting loop of area 2.0 × 10−3 m2 placed perpendicular to the field in each of the 10 ms intervals shown. (b) In which intervals is the emf not constant? Neglect the behaviour near the ends of 10 ms intervals.
उत्तर
Given:-
Area of the loop = 2.0 × 10−3 m2

The following conclusions can be made from the graph given above:
The magnetic flux at point O is 0.
The magnetic flux at point A is given by
ϕ2 = B.A = 0.01 × 2 × 10−3
= 2 × 10−5 ............[∵ ϕ1 = 0]
The change in the magnetic flux in 10 ms is given by
Δϕ = 2 × 10−5
The emf induced is given by
\[e = \frac{- ∆ \phi}{∆ t} = - \left( \frac{2 \times {10}^{- 5} - 0}{10 \times {10}^{- 3}} \right) = - 2 mV\]
The magnetic flux at point B is given by
ϕ3 = B.A = 0.03 × 2 × 10−3
= 6 × 10−5
The change in the magnetic flux in 10 ms is given by
Δϕ = 6 × 10−5 − 2 × 10−5 = 4 × 10−5
The emf induced is given by
\[e = - \frac{∆ \phi}{∆ t} = - 4 mV\]
The magnetic flux at point C is given by
ϕ4 = B.A = 0.01 × 2 × 10−3
= 2 × 10−5
The change in the magnetic flux in 10 ms is given by
Δϕ = (2 × 10−5 − 6 × 10−5 ) = − 4 × 10−5
The emf induced is given by
\[e = - \frac{∆ \phi}{∆ t} = 4 mV\]
The magnetic flux at point D is given by
ϕ5 = B.A = 0
The change in the magnetic flux in 10 ms is given by
Δϕ = 0 − 2 × 10−5
The emf induced is given by
\[e = \frac{- ∆ \phi}{∆ t} = - \frac{( - 2) \times {10}^{- 5}}{10 \times {10}^{- 3}} = 2 mV\]
(b) Emf is not constant in the intervals 10 ms‒20 ms and 20 ms‒30 ms.
APPEARS IN
संबंधित प्रश्न
(a) Obtain an expression for the mutual inductance between a long straight wire and a square loop of side an as shown in the figure.
(b) Now assume that the straight wire carries a current of 50 A and the loop is moved to the right with a constant velocity, v = 10 m/s.
Calculate the induced emf in the loop at the instant when x = 0.2 m.
Take a = 0.1 m and assume that the loop has a large resistance.

An aeroplane is flying horizontally from west to east with a velocity of 900 km/hour. Calculate the potential difference developed between the ends of its wings having a span of 20 m. The horizontal component of the Earth's magnetic field is 5 × 10–4 T and the angle of dip is 30°.
A metallic rod of ‘L’ length is rotated with angular frequency of ‘ω’ with one end hinged at the centre and the other end at the circumference of a circular metallic ring of radius L, about an axis passing through the centre and perpendicular to the plane of the ring. A constant and uniform magnetic field B parallel to the axis is presents everywhere. Deduce the expression for the emf between the centre and the metallic ring.
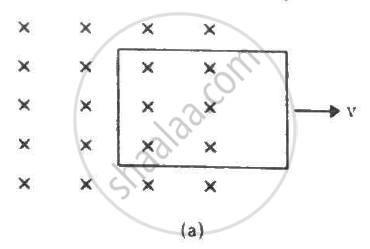
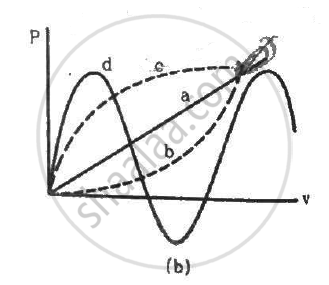
Figure shows a conducting loop being pulled out of a magnetic field with a speed v. Which of the four plots shown in figure (b) may represent the power delivered by the pulling agent as a function of the speed v?
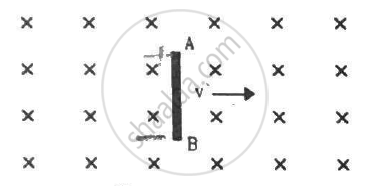
A rod AB moves with a uniform velocity v in a uniform magnetic field as shown in figure.
A conducting circular loop having a radius of 5.0 cm, is placed perpendicular to a magnetic field of 0.50 T. It is removed from the field in 0.50 s. Find the average emf produced in the loop during this time.
A square-shaped copper coil has edges of length 50 cm and contains 50 turns. It is placed perpendicular to a 1.0 T magnetic field. It is removed from the magnetic field in 0.25 s and restored in its original place in the next 0.25 s. Find the magnitude of the average emf induced in the loop during (a) its removal, (b) its restoration and (c) its motion.
Figure shows a conducting square loop placed parallel to the pole-faces of a ring magnet. The pole-faces have an area of 1 cm2 each and the field between the poles is 0.10 T. The wires making the loop are all outside the magnetic field. If the magnet is removed in 1.0 s, what is the average emf induced in the loop?
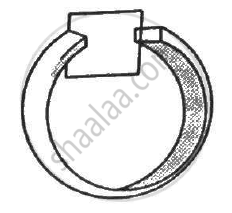
Figure shows a circular coil of N turns and radius a, connected to a battery of emf εthrough a rheostat. The rheostat has a total length L and resistance R. the resistance of the coil is r. A small circular loop of radius a' and resistance r' is placed coaxially with the coil. The centre of the loop is at a distance x from the centre of the coil. In the beginning, the sliding contact of the rheostat is at the left end and then onwards it is moved towards right at a constant speed v. Find the emf induced in the small circular loop at the instant (a) the contact begins to slide and (b) it has slid through half the length of the rheostat.
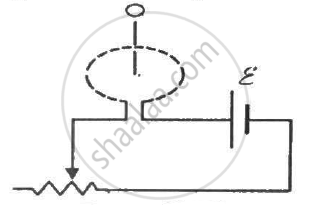
A circular coil of radius 2.00 cm has 50 turns. A uniform magnetic field B = 0.200 T exists in the space in a direction parallel to the axis of the loop. The coil is now rotated about a diameter through an angle of 60.0°. The operation takes 0.100 s. (a) Find the average emf induced in the coil. (b) If the coil is a closed one (with the two ends joined together) and has a resistance of 4.00 Ω, calculate the net charge crossing a cross-section of the wire of the coil.
The two rails of a railway track, insulated from each other and from the ground, are connected to a millivoltmeter. What will be the reading of the millivoltmeter when a train travels on the track at a speed of 180 km h−1? The vertical component of earth's magnetic field is 0.2 × 10−4 T and the rails are separated by 1 m.
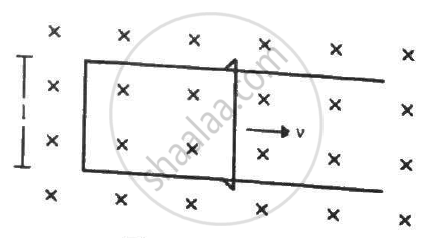
Figure shows a long U-shaped wire of width l placed in a perpendicular magnetic field B. A wire of length l is slid on the U-shaped wire with a constant velocity v towards right. The resistance of all the wires is r per unit length. At t = 0, the sliding wire is close to the left edge of the U-shaped wire. Draw an equivalent circuit diagram, showing the induced emf as a battery. Calculate the current in the circuit.
A rectangular frame of wire abcd has dimensions 32 cm × 8.0 cm and a total resistance of 2.0 Ω. It is pulled out of a magnetic field B = 0.020 T by applying a force of 3.2 × 10−5N (see the following figure). It is found that the frame moves with constant speed. Find (a) this constant speed, (b) the emf induced in the loop, (c) the potential difference between the points aand b and (d) the potential difference between the points c and d.
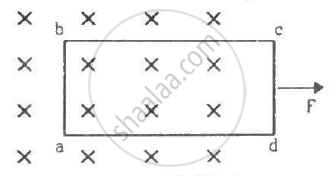
Figure shows a metallic square frame of edge a in a vertical plane. A uniform magnetic field B exists in the space in a direction perpendicular to the plane of the figure. Two boys pull the opposite corners of the square to deform it into a rhombus. They start pulling the corners at t = 0 and displace the corners at a uniform speed u. (a) Find the induced emf in the frame at the instant when the angles at these corners reduce to 60°. (b) Find the induced current in the frame at this instant if the total resistance of the frame is R. (c) Find the total charge which flows through a side of the frame by the time the square is deformed into a straight line.
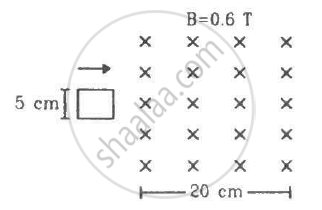
Figure shows a square loop of side 5 cm being moved towards right at a constant speed of 1 cm/s. The front edge enters the 20 cm wide magnetic field at t = 0. Find the total heat produced in the loop during the interval 0 to 30 s if the resistance of the loop is 4.5 mΩ.
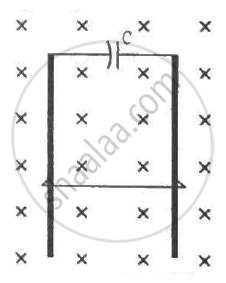
A wire of mass m and length l can slide freely on a pair of smooth, vertical rails (figure). A magnetic field B exists in the region in the direction perpendicular to the plane of the rails. The rails are connected at the top end by a capacitor of capacitance C. Find the acceleration of the wire neglecting any electric resistance.
An alternating emf of 110 V is applied to a circuit containing a resistance R of 80 Ω and an inductor L in series. The current is found to lag behind the supply voltage by an angle 8 = tan-1 (3/4). Find the :
(i) Inductive reactance
(ii) Impedance of the circuit
(iii) Current flowing in the circuit
(iv) If the inductor has a coefficient of self-inductance of 0.1 H, what is the frequency of the applied emf?
An induced e.m.f. is produced when a magnet is plunged into a coil. The strength of the induced e.m.f. is independent of ______.
When the rate of change oic current is unity, the induced emf is equal to ______.
